主要是我自己刷题的一些记录过程。如果有错可以指出哦，大家一起进步。
转载代码随想录
原文链接：
代码随想录
leetcode链接：90. 子集 II

题目：

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

示例：

示例 1：

输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

1 <= nums.length <= 10
-10 <= nums[i] <= 10

思路：

做本题之前一定要先做78.子集。这道题目和78.子集区别就是集合里有重复元素了，而且求取的子集要去重。

那么关于回溯算法中的去重问题，在40.组合总和II中已经详细讲解过了，和本题是一个套路。

剧透一下，后期要讲解的排列问题里去重也是这个套路，所以理解“树层去重”和“树枝去重”非常重要。

用示例中的[1, 2, 2] 来举例，如图所示： （注意去重需要先对集合排序）
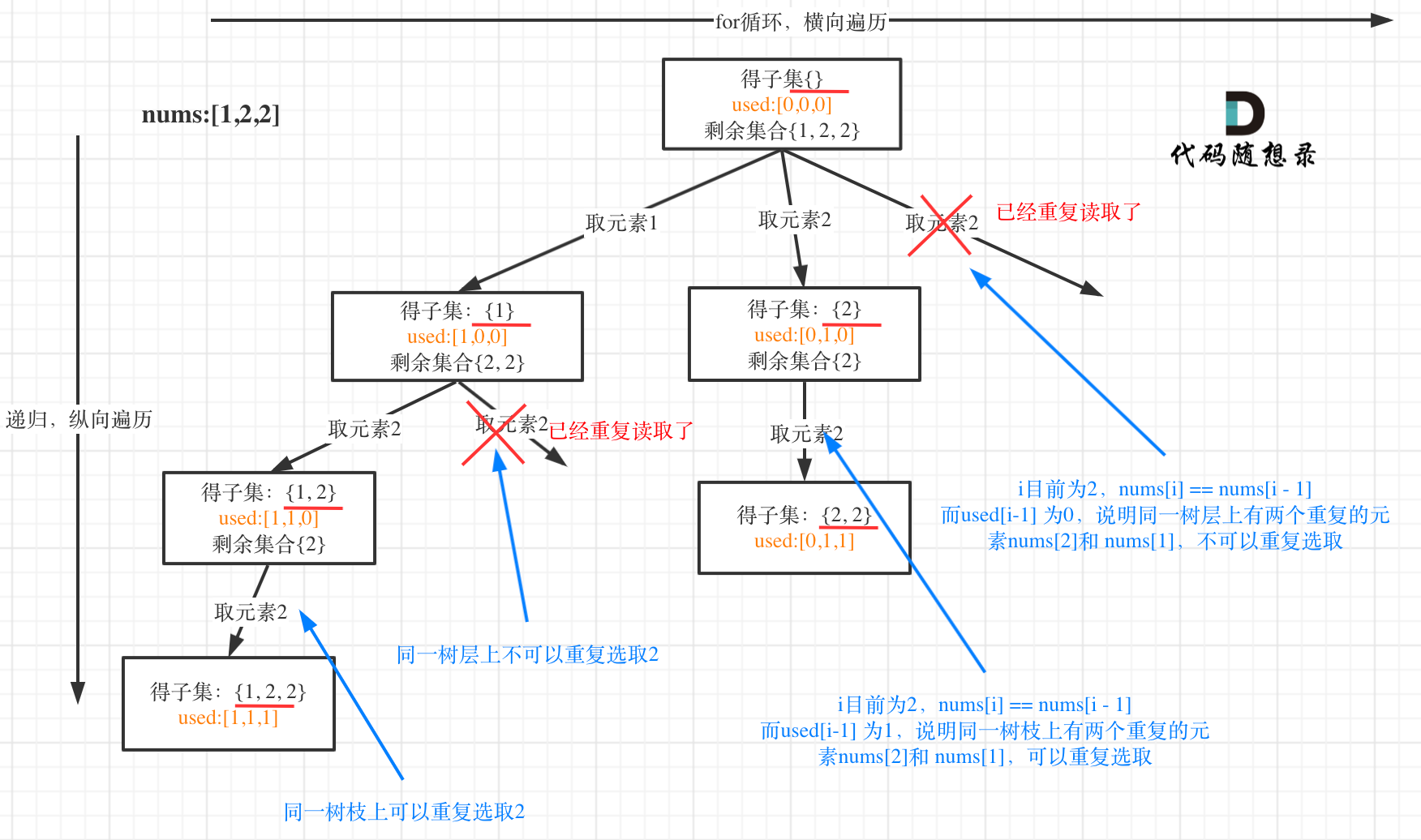从图中可以看出，同一树层上重复取2 就要过滤掉，同一树枝上就可以重复取2，因为同一树枝上元素的集合才是唯一子集！

本题就是其实就是回溯算法：求子集问题！的基础上加上了去重，去重我们在回溯算法：求组合总和（三）也讲过了，所以我就直接给出代码了：

C++代码如下：

class Solution {
private:vector> result;vector path;void backtracking(vector& nums, int startIndex, vector& used) {result.push_back(path);for (int i = startIndex; i < nums.size(); i++) {// used[i - 1] == true，说明同一树枝candidates[i - 1]使用过// used[i - 1] == false，说明同一树层candidates[i - 1]使用过// 而我们要对同一树层使用过的元素进行跳过if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue;}path.push_back(nums[i]);used[i] = true;backtracking(nums, i + 1, used);used[i] = false;path.pop_back();}}public:vector> subsetsWithDup(vector& nums) {result.clear();path.clear();vector used(nums.size(), false);sort(nums.begin(), nums.end()); // 去重需要排序backtracking(nums, 0, used);return result;}
};

使用set去重的版本。

class Solution {
private:vector> result;vector path;void backtracking(vector& nums, int startIndex) {result.push_back(path);unordered_set uset;for (int i = startIndex; i < nums.size(); i++) {if (uset.find(nums[i]) != uset.end()) {continue;}uset.insert(nums[i]);path.push_back(nums[i]);backtracking(nums, i + 1);path.pop_back();}}public:vector> subsetsWithDup(vector& nums) {result.clear();path.clear();sort(nums.begin(), nums.end()); // 去重需要排序backtracking(nums, 0);return result;}
};

补充

本题也可以不使用used数组来去重，因为递归的时候下一个startIndex是i+1而不是0。

如果要是全排列的话，每次要从0开始遍历，为了跳过已入栈的元素，需要使用used。

代码如下：

class Solution {
private:vector> result;vector path;void backtracking(vector& nums, int startIndex) {result.push_back(path);for (int i = startIndex; i < nums.size(); i++) {// 而我们要对同一树层使用过的元素进行跳过if (i > startIndex && nums[i] == nums[i - 1] ) { // 注意这里使用i > startIndexcontinue;}path.push_back(nums[i]);backtracking(nums, i + 1);path.pop_back();}}public:vector> subsetsWithDup(vector& nums) {result.clear();path.clear();sort(nums.begin(), nums.end()); // 去重需要排序backtracking(nums, 0);return result;}
};

总结

其实这道题目的知识点，我们之前都讲过了，如果之前讲过的子集问题和去重问题都掌握的好，这道题目应该分分钟AC。

当然本题去重的逻辑，也可以这么写

if (i > startIndex && nums[i] == nums[i - 1] ) {continue;
}

自己的代码

class Solution {vector>result;vectorpath;void dfs(vector& nums, vector& used, int startIndex) {// if (startIndex > nums.size())    return;result.push_back(path);for (int i = startIndex; i < nums.size(); ++i) {if (i > 0 && used[i-1] == false && nums[i] == nums[i - 1])     continue;path.push_back(nums[i]);used[i] = true;dfs(nums, used, i+1);used[i] = false;path.pop_back();}}public:vector> subsetsWithDup(vector& nums) {int size = nums.size();sort(nums.begin(), nums.end());vector used(nums.size(), false);dfs(nums, used, 0);return result;}
};