对于全连接层来说，其单层的参数量为 (输入维度 + 1) * 该层神经元个数。这是因为全连接层的每个神经元都需要一个 权重向量 和一个 偏置值 来计算其输出，权重向量 的长度就是 输入维度，偏置值 是一个标量。

若当前 network 有 hidden_layers 层 hidden layer，其中每层 hidden_layer 有 hidden_dim 维，则有：

Total_params=(input_dim+1)∗hidden_dim+(hidden_dim+1)∗hidden_dim∗(hidden_layers−1)+(hidden_dim+1)∗output_dimTotal\_params = (input\_dim + 1) * hidden\_dim + (hidden\_dim + 1) * hidden\_dim * (hidden\_layers - 1) + (hidden\_dim + 1) * output\_dimTotal_params=(input_dim+1)∗hidden_dim+(hidden_dim+1)∗hidden_dim∗(hidden_layers−1)+(hidden_dim+1)∗output_dim

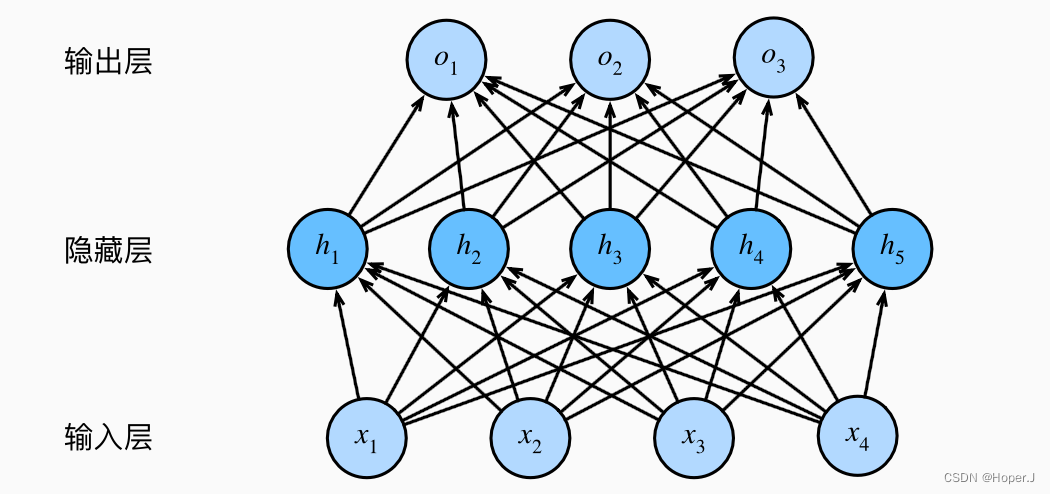
对于一个神经网络来说，其总参数量就是所有全连接层的参数量之和。例如，如果我们有一个神经网络，它有一个输入层（输入维度为 4），一个隐藏层（隐藏层神经元个数为 5），和一个输出层（输出维度为 3），那么它的总参数量就是：

输入层到隐藏层的全连接层：(4+1)∗5=25(4 + 1) * 5 = 25(4+1)∗5=25
隐藏层到输出层的全连接层：(5+1)∗3=18(5 + 1) * 3 = 18(5+1)∗3=18
总参数量：25+18=4325 + 18 = 4325+18=43

那么该如何创建多隐藏层的网络以及打印参数量呢？
这里举个例子说明：

import torch.nn as nninput_dim = 8
hidden_dim = 16
hidden_layers = 2
output_dim = 8# 为了简洁，舍去了 Relu()
network = nn.Sequential(nn.Linear(input_dim, hidden_dim),# 在函数的调用中，一个 * 表示将一个序列展开为单独的位置参数，这一行代码是列表推导，最终的表现是重复生成多个 hidden layer*[nn.Linear(hidden_dim, hidden_dim) for _ in range(hidden_layers-1)], nn.Linear(hidden_dim, output_dim))
# 打印总参数量
total_params = ((input_dim+1) * hidden_dim +(hidden_dim + 1) * hidden_dim * (hidden_layers - 1) +(hidden_dim + 1) * output_dim
)
print(f'Total params: {total_params}')

>> Total params: 552

当然，实际上你可以直接使用 pytorch 中的函数进行打印

total_params = sum(param.numel() for param in network.parameters())
print(f'Total params: {total_params}')

>> Total params: 552

进一步的，如果你想查看各层分别的参数量，你可以使用以下代码

for name, param in network.named_parameters():print(name, param.numel())

0.weight 128
0.bias 16
1.weight 256
1.bias 16
2.weight 128
2.bias 8

其中 weight 对应的是权重，bias是偏差。

参考链接：
图源自《动手学深度学习》
HW02 的 Sample code