P2568 GCD（欧拉函数，二维平面思想）
创始人
2025-05-29 01:14:38

题目描述

给定正整数 n，求 1≤x,y≤n 且 gcd(x,y) 为素数的数对 (x,y) 有多少对。

输入格式

只有一行一个整数，代表n。

输出格式

一行一个整数表示答案。

输入输出样例

输入 #1复制

4

输出 #1复制

4

说明/提示

样例输入输出 1 解释

对于样例，满足条件的 (x,y)为 (2,2)，(2,4)，(3,3)(4,2)。

数据规模与约定

  • 对于 100% 的数据，保证 1≤n≤107。

解析：

首先要先理解题意：gcd(x,y)是最大公约数。这道题的意思是最大公约数是一个素数。

如gcd（2，2） = 2，2为素数。

想到二维坐标，由二维坐标可以看出他们对称是以y=x；

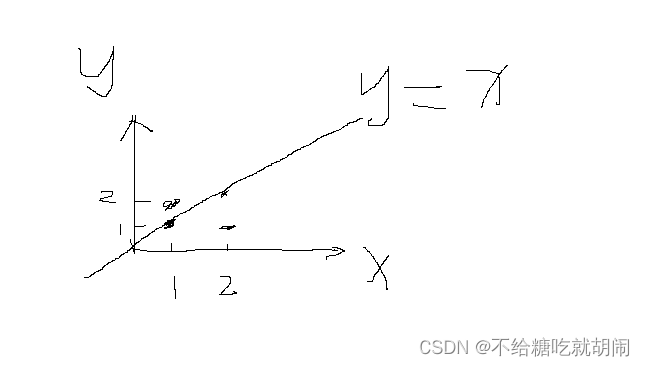
在这种条件下，公式这里可以进行化简

 

 这是就是求解在0~n/x（x为素数）相互互素的数。

而欧拉函数的定义就是：在n的范围内于n互素的个数。

这里就是有人会问了gcd（2，2） = 2它可以化成gcd(1,1) = 1的。

欧拉函数f(1) = 1;

这样子就可以成功求出来了。

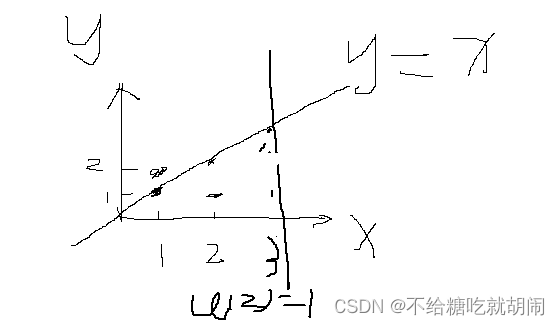
sum[3]为竖线左边的互素的个数。 

代码;

#include
using namespace std;
const int N = 1e7 + 10;
int prime[N];
int visit[N];
int pho[N];
long long sum[N];
int cnt = 0;
void get_ou(int n) {pho[1] = 1;for (int i = 2; i <= n; i++) {if (!visit[i]) {visit[i] = i;pho[i] = i - 1;prime[cnt++] = i;}for (int j = 0; j < cnt; j++) {if (prime[j] * i > N) {break;}visit[i * prime[j]] = prime[j];//表示最小的质因子if (i % prime[j] == 0) {pho[i * prime[j]] = pho[i] * prime[j];break;}pho[i * prime[j]] = pho[i] * pho[prime[j]];}}for (int i = 2; i < N; i++) {sum[i] = sum[i - 1] + pho[i];}
}
int main() {int n;cin >> n;get_ou(n);long long res = 0;for (int i = 0; i < cnt; i++) {res += sum[n / prime[i]] * 2 + 1; // 加1 是 还有（1，1）}cout << res<

词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。

上一篇：先正达将在科创板上会：拟募资650亿元，预计全年收入超2100亿元

下一篇：Unity 之 实现读取代码写进Word文档功能实现 -- 软著脚本生成工具

相关内容

热门资讯

城市住房产品力变化 | 探索“... 记者 田国宝 编者按：推开一扇门，有人看见三代同堂的烟火，有人撞见独自拼凑的晨昏，有人在精装样板间描...
破发股爱科赛博5高管拟减持 2... 中国经济网北京6月6日讯 爱科赛博(688719.SH)昨晚发布董事、高级管理人员减持股份计划公告。...
2025年前5月私募证券基金备... 2025年私募证券基金市场展现出强劲复苏势头。前5个月全行业累计备案私募证券基金4361只，较去年同...
始于雷军、困于罗永浩、终于董明... 在孟羽童和董明珠“世纪和解”重回格力直播后，沉寂了近一年的王自如在社交平台露面了。 6月5日晚，王自...
霸王茶姬首份成绩单背后，如何从... 如今的新茶饮市场高度内卷，价格战频发，霸王茶姬凭什么能做到稳健增长？文｜《中国企业家》记者胡楠楠编辑...
金陵饭店2024年净利润下滑4... 本报记者 李贝贝 上海报道2024年，金陵饭店股份有限公司（下称“金陵饭店”，601007.SH）归...
3年卖掉69座电站！林洋能源再... 本报（chinatimes.net.cn）记者李佳佳 李未来 北京报道近期，江苏林洋能源股份有限公司...
高考考点：二桃杀三士 如何应对... 祝各位考生高考节快乐。上次讲崔杼弑其君，星空君故意漏了一个细节。齐庄公死后，著名的退居二线的大夫晏婴...
非农数据提振市场，美国三大股指... 美股周五收高，道指上涨逾400点，标普500指数突破6000点整数关口。三大股指本周均录得涨幅。Wi...
美股上攻，黄金下跌超1% 美股... 2025.06.07本文字数：2393，阅读时长大约4分钟作者 |第一财经 樊志菁*三大股指涨超1%...
加力支持 精准滴灌 多方协同—...   新华社北京6月6日电 题：加力支持 精准滴灌 多方协同——金融护航外贸发展观察   新华社记者姚...
卖出600万只枕头的亚朵，栽在... 「核心提示」一只枕套，将加盟商和亚朵之间利益共生又充满矛盾的关系摆到了台面上。作者 |詹方歌邢昀一年...
“天价耳环事件”最新消息！“黄... 近期，因“天价耳环”事件备受关注的黄杨钿甜及其父亲杨伟持续引发热议。有网友发现其父杨伟在公开回应前，...
年轻人涌入医院买面包？为啥医院... 说起最近几年，各种消费热点中有一类非常特殊，这就是医院成为了不少消费的热点，各种中药咖啡、中药饮料、...
金穗春操纵股票遭证监会罚没过亿... 6月6日晚间，证监会披露的一则行政处罚决定书（2025 59号）显示，金穗春（男）操纵股票被证监会罚...
证监会核准中央汇金成为8家公司... 南财早新闻，早听早知道。1、上交所召开高分红重回报暨上市公司价值提升座谈会。上交所相关负责人表示，未...
信托业破局价格“内卷”：少赚吆... 1万元就可以做一单资产证券化业务——信托本源业务的低价“内卷”，正困扰着信托公司。 随着信托业转型加...
每周股票复盘：爱博医疗（688... 截至2025年6月6日收盘，爱博医疗（688050）报收于71.05元，较上周的71.41元下跌0....
大转向！外资，爆买！ 大转向如... 外资突然出现重大转变。在连续四个月净卖出后，外资在5月大举押注亚洲股市。据伦敦证券交易所集团(LSE...
不想对话！特朗普余气未消，特斯... 在双方爆发激烈“口水战”后，美国总统特朗普与特斯拉首席执行官（CEO）马斯克并未如外界期望的那样在周...
惊天大骗局，一万人踩雷 惊天大... 一万多人辛苦一辈子的血汗钱瞬间化为乌有。这再次说明了，天上不会掉馅饼。所有的投资都要基于常识，正如中...
广州农商银行60后副行长再担重... 担任广州农商银行副行长三年多后，李亚光再添职务，其首席信息官的任职资格获批。湘财Plus注意到，李亚...
标普500收复6000点！美股... *三大股指涨超1%；*加拿大产区大火持续，原油延续反弹；*特斯拉反弹超3%，市场关注特朗普与马斯克关...
诺诚健华涨2.42%，成交额1... 6月6日，诺诚健华涨2.42%，成交额1.28亿元，换手率2.01%，总市值432.89亿元。 异动...
远光软件跌0.34%，成交额1... 6月6日，远光软件跌0.34%，成交额1.72亿元，换手率1.72%，总市值111.83亿元。 异动...
非农数据提振市场，美国三大股指... 　　中新经纬6月7日电 美股周五收高，道指上涨逾400点，标普500指数突破6000点整数关口。三大...
每周股票复盘：招商银行（600... 截至2025年6月6日收盘，招商银行（600036）报收于44.47元，较上周的43.43元上涨2....
小阔集团董事长尹阔：民营经济促... 中国经济网北京6月6日讯（记者　李方）“民营经济促进法犹如一颗‘定心丸’，为我们营造了一个稳定、公平...
Circle纽交所上市：大涨1... 雷递网 雷建平 6月6日 USDC稳定币发行商Circle（股票代码为：“CRCL”）昨日在纽交所上...
招商银行成功发行50亿绿色金融... 2025年6月5日，在第54个“世界环境日”到来之际，招商银行在全国银行间债券市场成功簿记发行绿色金...