106.从中序与后序遍历序列构造二叉树

前序和中序可以唯一确定一棵二叉树，后序和中序可以唯一确定一棵二叉树，而前序和后序不能确定一棵二叉树。

有个问题没解决：

class Solution {Map map=new HashMap<>();public TreeNode buildTree(int[] inorder, int[] postorder) {for(int i=0;imap.put(inorder[i],i);}return FindNode(inorder,0,inorder.length,postorder,0,postorder.length);}public TreeNode FindNode(int[] inorder,int inBegin,int inEnd,int[] postorder,int postBegin,int postEnd){if(inBegin>=inEnd||postBegin>=postEnd){return null;}int index=map.get(postorder[postEnd-1]);//int index=map.get(postorder[postorder.length-1]);这样写报错了，但是不知道为啥TreeNode root=new TreeNode(inorder[index]);int leftlength=index-inBegin;root.left=FindNode(inorder,inBegin,index,postorder,postBegin,postBegin+leftlength);root.right=FindNode(inorder,index+1,inEnd,postorder,postBegin+leftlength,postEnd-1);return root;}
}

在代码中注释的那部分出现了错误，报错是：（没解决……）

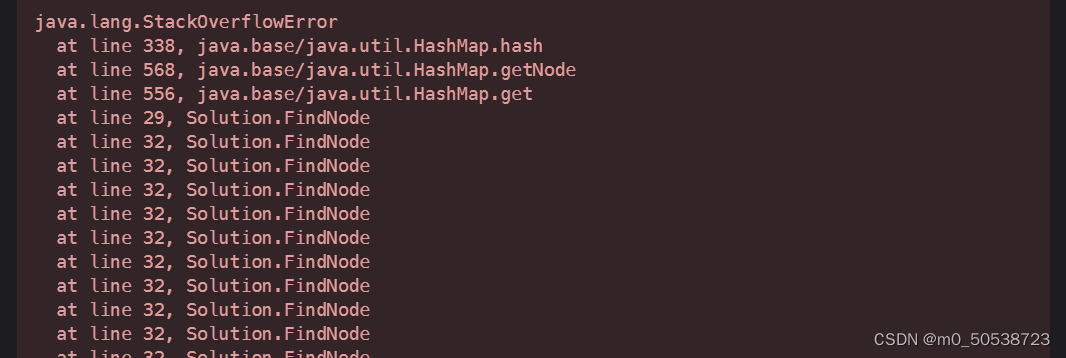
这道题的map这里，get方法得到的是key对应的value值，所以在前面是把结点的值作为key，把坐标作为value

105.从前序与中序遍历序列构造二叉树(和上个题一样)

class Solution {Map map=new HashMap<>();public TreeNode buildTree(int[] preorder, int[] inorder) {for(int i=0;imap.put(inorder[i],i);}return FindNode(preorder,0,preorder.length,inorder,0,inorder.length);}public TreeNode FindNode(int[] preorder,int preBegin,int preEnd,int[] inorder,int inBegin,int inEnd){if(preBegin>=preEnd||inBegin>=inEnd){return null;}int index=map.get(preorder[preBegin]);TreeNode root=new TreeNode(inorder[index]);int leftlen=index-inBegin;root.left=FindNode(preorder,preBegin+1,preBegin+1+leftlen,inorder,inBegin,index);root.right=FindNode(preorder,preBegin+1+leftlen,preEnd,inorder,index+1,inEnd);return root;}
}

654. 最大二叉树

感觉这个题特别难，但是看了答案发现，和其前面的两个题很像，只不过这道题的根节点是找最大值作为根节点，然后由根节点将数组分成左右两部分，也就是左右子树，相当于把前面的题的其中一个遍历序列隐藏了，但是思路仍然是一样的。仍然还需要两个指针，只是得到根节点的方法比较简单

class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {return BuildTree(nums,0,nums.length);}public TreeNode BuildTree(int[] nums,int leftIndex,int rigthIndex){if(rigthIndex-leftIndex<1){return null;}if(rigthIndex-leftIndex==1){return new TreeNode(nums[leftIndex]);}int maxIndex=leftIndex;int maxValue=nums[maxIndex];for(int i=leftIndex+1;i//if(maxValuemaxIndex=i;maxValue=nums[i];}}TreeNode root=new TreeNode(maxValue);root.left=BuildTree(nums,leftIndex,maxIndex);root.right=BuildTree(nums,maxIndex+1,rigthIndex);return root;}
}

617. 合并二叉树

递归：

class Solution {public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {if(root1==null) return root2;if(root2==null) return root1;root1.val+=root2.val;root1.left=mergeTrees(root1.left,root2.left);root1.right=mergeTrees(root1.right,root2.right);return root1;}
}

非递归：

class Solution {public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {if(root1==null) return root2;if(root2==null) return root1;Stack stack=new Stack<>();stack.push(root2);stack.push(root1);while(!stack.isEmpty()){TreeNode node1=stack.pop();TreeNode node2=stack.pop();node1.val+=node2.val;if(node1.right!=null&&node2.right!=null){stack.push(node2.right);stack.push(node1.right);}if(node1.right==null&&node2.right!=null){node1.right=node2.right;}if(node1.left!=null&&node2.left!=null){stack.push(node2.left);stack.push(node1.left);}if(node1.left==null&&node2.left!=null){node1.left=node2.left;}}return root1;}
}

注意：
1、这道题还可以用队列的方式，队列的话，就不用先让右子树入队，然后再让左子树入队了
2、再说一遍：栈的方法是——push、pop，队列的出入方法是——offer、poll
3、还有判空的方法是stack.isEmpty()别写错了

700. 二叉搜索树中的搜索

递归：（但是没有用到二叉搜索树的特点）

class Solution {public TreeNode searchBST(TreeNode root, int val) {if(root==null||root.val==val){return root;}TreeNode left=searchBST(root.left,val);if(left!=null) return left;TreeNode right=searchBST(root.right,val);return right;}
}

这里要注意，不能写成：return searchBST(root.left,val)；和return searchBST(root.right,val)；因为要等到所有节点都遍历完之后再返回，否则下面的搜索右子树的语句永远不会执行。他执行的前提是左子树没有搜索到节点，所以需要判断左子树是否搜索到了！

递归：（用到二叉搜索树的特点）

public TreeNode searchBST(TreeNode root, int val) {if(root==null||root.val==val){return root;}if(root.val

public TreeNode searchBST(TreeNode root, int val) {while(root!=null){if(root.val==val) return root;else if(root.val

class Solution {public boolean isValidBST(TreeNode root) {return validBST(Long.MIN_VALUE,Long.MAX_VALUE, root);}public boolean validBST(long lower,long upper,TreeNode root){if(root==null) return true;if(root.val<=lower||root.val>=upper) return false;return validBST(lower,root.val,root.left)&&validBST(root.val,upper,root.right);}
}

class Solution {long prev=Long.MIN_VALUE;public boolean isValidBST(TreeNode root) {if(root==null) return true;if(!isValidBST(root.left)){return false;}if(root.val<=prev) return false;prev=root.val;return isValidBST(root.right);}
}

class Solution {TreeNode pre;int min=Integer.MAX_VALUE;public int getMinimumDifference(TreeNode root) {if(root==null) return 0;traversal(root);return min;}public void traversal(TreeNode root){if(root==null) return;traversal(root.left);if(pre!=null){min=Math.min(min,root.val-pre.val);}pre=root;traversal(root.right);}
}

class Solution {TreeNode pre;Stack stack=new Stack<>();public int getMinimumDifference(TreeNode root) {if(root==null) return 0;int min=Integer.MAX_VALUE;TreeNode cur=root;while(cur!=null||!stack.isEmpty()){if(cur!=null){stack.push(cur);cur=cur.left;}else{cur=stack.pop();if(pre!=null){min=Math.min(min,cur.val-pre.val);}pre=cur;cur=cur.right;}}return min;}
}

class Solution {List answer=new LinkedList<>();int maxCount,count,base=0;public int[] findMode(TreeNode root) {dfs(root);int[] mode=new int[answer.size()];for(int i=0;imode[i]=answer.get(i);}return mode;}public void dfs(TreeNode root){if(root==null) return;dfs(root.left);update(root.val);dfs(root.right);}public void update(int x){if(x==base){count++;}else{base=x;count=1;}if(count==maxCount){answer.add(x);}if(count>maxCount){maxCount=count;answer.clear();answer.add(x);}}
}

class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if(root==null||root==p||root==q){return root;}TreeNode left=lowestCommonAncestor(root.left,p,q);TreeNode right=lowestCommonAncestor(root.right,p,q);if(left==null&&right==null) return null;else if(left==null&&right!=null) return right;else if(left!=null&&right==null) return left;else return root;}
}