《Protein Actions Principles and Modeling》-《蛋白质作用原理和建模》

本人能力有限，如果错误欢迎批评指正。

第五章：Folding and Aggregation Are Cooperative Transitions

            （折叠和聚合是同时进行的）

-蛋白质和肽具有协同性的螺旋-线团转变

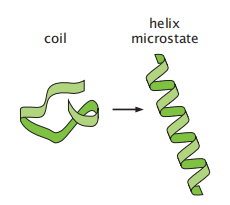
图5.4 一些蛋白质经历了从螺旋-线团转变。线圈状态是一个大的无序构象的集合（许多微观状态）。螺旋是一个相对独特的构象（单一的微观状态）。

有些类型的聚合物可以再实验中观察到两种可区分的状态：一种是线团(coil)状态，这是一种含有大量无序结构的集合，而另一种则是由单一构象组成的螺旋状态集合(图5.4)。改变溶剂条件或温度可以导致这些聚合物进行线团状态和螺旋之间的急剧转变。那么，是什么导致了这种构象的变化？

多肽的构象可以表示为一维二进制字符串：“c”表示线团构象的每个单元（例如每个残基），“h”表示螺旋构象的每个残基。例如，一个16链的一个特殊构象可以表示为:

现在，我们需要建立一个螺旋-线团转变的物理模型，从中我们可以计算出实验中可观察到的性质。通常，容器中所有分子的平均值是最容易测量的。而我们的目标是计算概率分布上的平均值。不同的分子将有n=1,2,3…个螺旋单位。我们想知道一条有n个单位的蛋白质的平均螺旋:

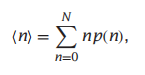
为了计算，，我们需要知道概率分布p (n)。它是由

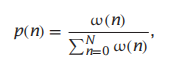
其中，ω(n)是占螺旋构象中具有n个单位的链的总体的统计权重(statistical weight)。统计权重是一个相对数量；它不需要像概率一样被归一化为1。公式5.4显示了概率（标准化量）与统计权重之间的关系。方程5.4的分母中的一个关键量是配分函数Q:

这是系统中所有可能状态的统计权重的和，其中状态n在这种情况下指的是具有n个螺旋旋转的构象集合。因此，我们建模的目标是找到一种计算ω(n)的方法，即系统状态n的统计权重。现在，我们考虑这三个层次的统计权重：(1)我们需要对链中的每个h或c个残基进行统计权重。(2)我们需要对整个链的每个微观状态的统计权重，即，对于一个特定的h和c单位的序列。(3)我们需要将组成感兴趣的链宏观状态的任何微观状态的统计权重相加。宏观状态通常是指一些实验上可观测到的状态。例如，变性状态是微观状态的宏观状态集合。

(1)每个h或者c的统计权重。首先，我们将每个线团单元c的统计权重定义为1。因为只有统计权重的比率对计算概率很重要，所以我们可以任意的选择这个统计权重。然后我们给每个螺旋氨基酸残基h分配一个统计权重s。我们可以把s当做包含了一个螺旋和一个线团单元的平衡常数。这些单元的化学性质以及氨基酸链所处的环境温度性质都会影响到s。溶液的环境以及温度有时候会导致一个氨基酸更倾向于形成螺旋构象。如果s>1,那么这个时候形成螺旋的倾向性大于形成线团的倾向性。反之亦然。s=1，则说明二者的倾向性相同。在现实中，不同的氨基酸会有不同的s值，但在这里我们将其简单化-人为规定所有的氨基酸具有相同的s值。

(2)包含了h以及c单元的链的统计权重。我们可以通过BOX 5.1的方式利用概率规则描述构造Q。现在，我们将这个推理用于不同模型的计算。为了研究协同性的本质，我们先从假设一个模型没有协同性开始。

====================================================

BOX5.1关于概率以及平均的说明

让我们回顾一下两个概率规律(1):如果状态A和状态B是互斥的，如果您想计算查看状态A或状态B的统计权重，那么ω(A或 B) = ω(A) + ω(B)(2):如果状态A和B是独立的，这两个状态A和B的统计权重为 ω（A和B）= ω(A)ω(B).我们将相应地增加或乘以统计权重和概率。这里有一个对计算平均值的数学方法。配分函数形式为：

在这样的表达式中，术语sn是具有n个的螺旋的统计权重，对应的概率为

那么平均的螺旋数量为

====================================================

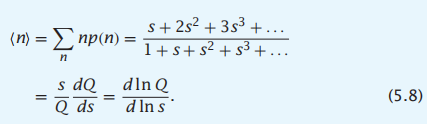
第一个可以尝试的模型：独立单元(:independent units)

这个模型每个c单元和h单元与其他单元相独立，那么所有的微观状态的配分函数为

因为链中的每个单元都可以是c或h，而这些又都是互斥的。因此我们可以获得1+s。然后，然后1+s有N次幂因为链中有N个单元。因为我们在寻找统计权重，单元1和单元2和单元3…都处于特定的状态。将方程5.9代入方程5.8得到平均螺旋度：

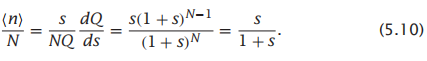
现在，假设进行溶剂或温度可以系统变化的一系列实验。每个实验对应于一个不同的s值，即螺旋倾向。方程5.10对这个独立单元模型预测，平均螺旋度作为s的函数会逐渐变化，但不是s型曲线(图5.5)。这个独立单元模型不能体现平均螺旋度与s的s型形状，也不能展示这个函数（单位螺旋度）随着N的变化而变得更陡，这两者都是在实验中观察到。因此，接下来我们需要考虑一个更好的螺旋-线团协同性的模型。

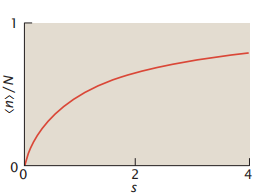
图5.5 如果单位是独立的，则平均螺旋度只会随着螺旋倾向的增加而逐渐变化。在独立单元模型中，如果s因温度或溶剂的变化而变化，则平均螺旋度会随着s的变化逐渐变化。每个单体的螺旋度曲线的斜率并不依赖于链长N（因为单体是独立的）。但实验表明，随着N的增大，转变会变得更尖锐。

第二个模型：双态模型(two-state)
现在，让我们尝试一个不同的模型。在这个模型中，链要么是全线团（cccc…c），要么是全螺旋（hhhh…h），并且没有其他微观状态。这个模型具有最大协同性-只有两个状态。如果任何一个单元处于h状态，则所有单元都处于该状态。因此，它的配分函数是

也就是说蛋白质要么有所有的线团，统计权重为1N，或所有的螺旋，权重为sN，并且这两个链状态是相互排斥的。将方程5.11代入螺旋度方程式5.8，得到

该模型预测/N与s的关系是一个s型函数，并且随着N的增加而变得更陡（图5.6）。这些特征在质量上是正确的，但在数量上，这种变化过于陡峭。在实验中，这种陡度只适用于N>1000的链。

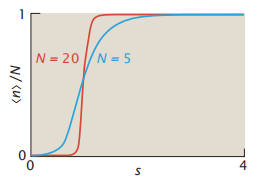
图5.6 双态模型预测螺旋度随s的变化会急剧变化。但是预测的对N的依赖性比在实验中看到的要大得多。

所以，让我们考虑第三个模型，该模型最初是由于约翰·谢尔曼(John Schellman)提出的，它介于这两个极端之间。在下面的章节中，我们使用术语“双态（two state）”，但这不是刚才的零中间种群的极端状态，而是也用于中间种群相对较小的情况。在谢尔曼模型中，螺旋的形成包括两个方面：起始和增值(initiation and propagation)。

谢尔曼模型将螺旋-线团的转变描述为成核后的生长(Nucleation Followed by Growth)

谢尔曼模型将螺旋定义为不间断h的延伸。为了使数学上保持简单，假设在链中最多存在一个螺旋段（任意长度为n）。这种单螺旋假设(single-helix approximation)通常适用于溶液中小于20氨基酸长度的肽。在这个模型中，c的统计权重是1，h的统计权重是s。此外，还有一个是成核参数σ(开始螺旋的平衡常数)被引入这个模型。也就是说，螺旋中的每一个“第一个”h都分配了一个统计权重σs而后边的h状态权重为s。Box5.2展示了对不同链进行统计权重。

====================================================

BOX5.2：统计权重的示例

====================================================

我们可以计算所有构象的统计权重ωn，链任何位置上的单一的螺旋包含n个氨基酸：

这相对于所有残基都处于线团状态的链。方程5.13中的因子（N−n + 1）计算了在N长度的链中具有n个残基的螺旋单元（n > 0）可能起始位置的数量。

现在，我们通过将ωn转换为除以所有螺旋长度的和Q1（其中下标1表示单个螺旋，以区别于下面的螺旋束模型）来获得概率p (n)：

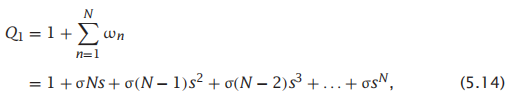
其中，前导项1是线圈状态的统计权重。所以，一个链有n个螺旋残基的概率是

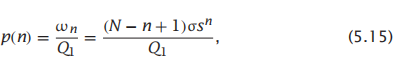
并且拥有一个全线团链的概率是p(0) = 1/Q1。

我们也可以计算出平均螺旋度(average helicity)为

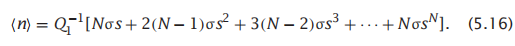
下面是如何使用谢尔曼螺旋-线团模型。我们得到了最大螺旋长度N、成核参数σ和传播参数，可以使用公式5.14来计算配分函数Q1。然后使用公式5.15来计算你感兴趣的任何p (n)，包括全螺旋分子的p (N)。为了与实验进行比较，你需要公式5.16中的平均螺旋度。（使用标准的统计力学表达式，您还可以采用方程5.16的二阶导数来计算螺旋长度的方差。）

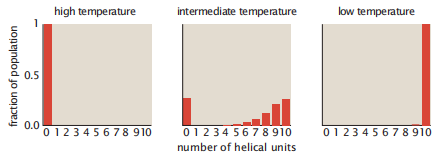
图5.7 螺旋-线团转变的例子，包含了有限的中间状态种群。使用公式5.15计算的是N=10，σ=10−4，和s的各种值。链在高温条件下（s = 0.02）条件下全线团，在低温条件下全螺旋（s = 200）。在中等温度（s=2.5）（例如方程5.14给出Q1=3.64），所有中间状态都比线圈（i = 0）或螺旋（i = 10）状态少。

对于参数σ和s的值，舍尔曼模型可以预测两态协同性。图5.7显示了三个不同的s值的螺旋长度的分布。在这个例子中，中间状态i比全线团/全螺旋状态的填充要少得多。也就说在转变中点，p1 > pi < pN。当成核困难时（即当σ<<1），有利于扩散（即当s > 1）时，就会发生双态行为。在这种情况下，线圈因为其较大的构象熵而存在。螺旋因为沿链的多个氢键单位的低能量而存在。在全螺旋和全线圈之间的中间状态则不易存在。而言之，当成核困难时，你会发现常出翔线团分子或长螺旋，而非短螺旋。形成一个螺旋旋转的熵是非常昂贵的，但如果链形成足够多的螺旋旋转，那么它在能量上就变得有利。

可以通过加热螺旋结构进行变性

我们将螺旋-线团的平衡表示为两个参数σ和s的关系。然而，螺旋-线团种群如何与实验上可控的变量，如温度或变性剂浓度具有什么关系才是值得去关注的。螺旋-线团平衡通过s=(T)和σ = σ(T)来搭建与温度的关系。你可以用平衡系数σ和s对应的焓H和熵S来表示平衡系数σ和s的与温度依赖关系。这样做可以为σ和s. s (T)的微观物理基础提供有用的见解，可以用ΔG (T) =−RTlnK=H−TS来表示形成一个螺旋的自由能：

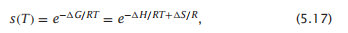
其中焓ΔH（=εhb，其中εhb< 0）是会因为螺旋的形成而变小。假设每个残基都可以获得z局部构象（或异构体）态（例如，我们可以对螺旋态、β链态和螺旋态的z = 3进行简单的估计），熵ΔS(T) = −Rln(z − 1)则会因为螺旋上的残基增多而降低。换句话说，非螺旋氨基酸的熵是S = Rln（z−1），而螺旋氨基酸的熵是S = Rln 1 = 0，因此每个氨基酸从螺旋到螺旋转变的ΔS=−Rln（z−1）发生变化。R是气体常数，T是绝对温度。将螺旋增加一个残基的对焓变是有利的（负的），对熵变是不利的（负的）。因此，参数与温度的关系是由给出的

同样，成核也可以用焓εhb来表示：

方程5.18和5.19用能量和熵分量的模型来表示σ(T)和s (T)。这些局部术语描述了成核相对于增殖在熵上是不利的。成核的代价涉及到固定构象的熵，以便在氨基酸i的C=O基和氨基酸i + 4的N-H基之间形成氢键。这四个残基中的第一个可以指向任意方向；然后接下来的三个是固定的，因此因子（z−13。相反，增殖的代价涉及到只固定一个残差的熵。由于我们的模型的简单性，这些因素只是近似的，但它们揭示了在熵上成核不如增殖有利的原理。

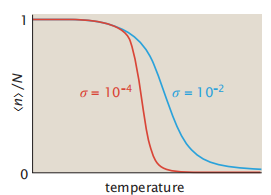
图5.8 谢尔曼螺旋-线团模型预测了一个急剧的热转变。这个计算是一个N=10螺旋模型，其中每个键的方向为z = 5，每个螺旋键的能量为εhb/R =−500K，以及两个不同的σ值。螺旋残基的平均数目由公式5.16计算得出。σ的值越小，过渡就越尖锐。

图5.8显示是温度T的s型函数：螺旋随着温度的升高而熔化。它还表明，随着σ变得更小（即，当成核的能量成本非常高时），跃迁变得更尖锐。

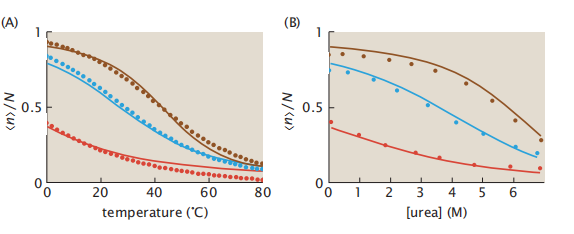
图5.9 螺旋-螺旋模型可以根据温度或尿素浓度模拟螺旋变性，链长为N=50（棕色）、N=26（蓝色）和N=14（红色）：(A)热变性数据；(B)尿素变性。

图5.9显示，这个简单的螺旋线圈理论适合平均螺旋度作为温度函数或变性剂（尿素）浓度函数的实验测量。那么我们要如何确定σ和s的值呢？不同的氨基酸有不同的螺旋倾向s。（σ的值，在不同的模型中范围从10−2到10−4，不会过分地受到氨基酸类型的影响）。

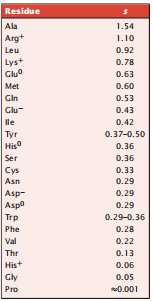
表5.1 不同氨基酸的螺旋倾向。

表5.1给出了一个实验值的总结。一般来说，丙氨酸具有形成螺旋的高倾向，而脯氨酸是螺旋破坏者。有时，为了探索原理问题，我们对σ使用单一值，对所有氨基酸使用单一值，就像我们之前做的那样。

-------------------------------------------

欢迎点赞收藏转发！

下次见！