【2022年蓝桥杯真题之带权并查集问题】推导部分和

创始人

2025-05-31 07:13:00

⭐️前面的话⭐️

【2022年蓝桥杯真题之带权并查集问题】推导部分和
对于一个长度为 NNN 的整数数列 A1,A2,⋯ANA_1, A_2, \cdots A_NA1,A2,⋯AN, 小蓝想知道下标 lll 到 rrr 的部分和 ∑i=lr=Al+Al+1+⋯+Ar\sum_{i=l}^r=A_l+A_{l+1}+\cdots+A_r∑i=lr=Al+Al+1+⋯+Ar 是多少?
然而, 小蓝并不知道数列中每个数的值是多少, 他只知道它的 MMM 个部分和的值。其中第 iii 个部分和是下标 lil_ili 到 rir_iri 的部分和 ∑j=liri=\sum_{j=l_i}^{r_i}=∑j=liri= Ali+Ali+1+⋯+AriA_{l i}+A_{l i+1}+\cdots+A_{r i}Ali+Ali+1+⋯+Ari, 值是 SiS_iSi 。解题代码：Java, C++。

📒博客主页：未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创，CSDN首发！
📆首发时间：🌴2023年3月20日🌴
✉️坚持和努力一定能换来诗与远方！
💭推荐书籍：📚《算法》，📚《算法导论》
💬参考在线编程网站：🌐牛客网🌐力扣
博主的码云gitee，平常博主写的程序代码都在里面。
博主的github，平常博主写的程序代码都在里面。
🍭作者水平很有限，如果发现错误，一定要及时告知作者哦！感谢感谢！

📌导航小助手📌

⭐️推导部分和⭐️
- 🔐题目详情
- - 问题描述
  - 输入格式
  - 输出格式
  - 样例输入
  - 样例输出
  - 评测用例规模与约定
  - 运行限制
- 💡解题思路
- 🔑源代码
🌱总结

⭐️推导部分和⭐️

🔐题目详情

问题描述

对于一个长度为 NNN 的整数数列 A1,A2,⋯ANA_1, A_2, \cdots A_NA1,A2,⋯AN, 小蓝想知道下标 lll 到 rrr 的部分和 ∑i=lr=Al+Al+1+⋯+Ar\sum_{i=l}^r=A_l+A_{l+1}+\cdots+A_r∑i=lr=Al+Al+1+⋯+Ar 是多少?
然而, 小蓝并不知道数列中每个数的值是多少, 他只知道它的 MMM 个部分和的值。其中第 iii 个部分和是下标 lil_ili 到 rir_iri 的部分和 ∑j=liri=\sum_{j=l_i}^{r_i}=∑j=liri= Ali+Ali+1+⋯+AriA_{l i}+A_{l i+1}+\cdots+A_{r i}Ali+Ali+1+⋯+Ari, 值是 SiS_iSi 。

输入格式

第一行包含 3 个整数 N、MN 、 MN、M 和 QQQ 。分别代表数组长度、已知的部分和数量和询问的部分和数量。
接下来 MMM 行, 每行包含 3 个整数 li,ri,Sil_i, r_i, S_ili,ri,Si 。
接下来 QQQ 行, 每行包含 2 个整数 lll 和 rrr, 代表一个小蓝想知道的部分和。

输出格式

对于每个询问, 输出一行包含一个整数表示答案。如果答案无法确定, 输出 UNKNOWN。

样例输入

样例输出

15
6
UNKNOWN

评测用例规模与约定

对于 10%10 \%10% 的评测用例, 1≤N,M,Q≤10,−100≤Si≤1001 \leq N, M, Q \leq 10,-100 \leq S_i \leq 1001≤N,M,Q≤10,−100≤Si≤100
对于 20%20 \%20% 的评测用例, 1≤N,M,Q≤20,−1000≤Si≤10001 \leq N, M, Q \leq 20,-1000 \leq S_i \leq 10001≤N,M,Q≤20,−1000≤Si≤1000
对于 30%30 \%30% 的评测用例, 1≤N,M,Q≤50,−10000≤Si≤1 \leq N, M, Q \leq 50,-10000 \leq S_i \leq1≤N,M,Q≤50,−10000≤Si≤ 10000 。
对于 40%40 \%40% 的评测用例, 1≤N,M,Q≤1000,−106≤Si≤1061 \leq N, M, Q \leq 1000,-10^6 \leq S_i \leq 10^61≤N,M,Q≤1000,−106≤Si≤106
对于 60%60 \%60% 的评测用例, 1≤N,M,Q≤10000,−109≤Si≤1 \leq N, M, Q \leq 10000,-10^9 \leq S_i \leq1≤N,M,Q≤10000,−109≤Si≤ 10910^9109 。
对于所有评测用例, 1≤N,M,Q≤105,−1012≤Si≤1 \leq N, M, Q \leq 10^5,-10^{12} \leq S_i \leq1≤N,M,Q≤105,−1012≤Si≤ 1012,1≤li≤ri≤N,1≤l≤r≤N10^{12}, 1 \leq l_i \leq r_i \leq N, 1 \leq l \leq r \leq N1012,1≤li≤ri≤N,1≤l≤r≤N 。数据保证没有矛盾。

运行限制

最大运行时间：3s
最大运行内存: 512M

💡解题思路

根据前缀和的经验，我们知道区间[l,r][l, r][l,r]的和可以表示为d[r]−d[l−1]d[r] - d[l - 1]d[r]−d[l−1]，其中ddd为前缀和数组，这道题差不多是反着过来的，题目会给定若干组区间和，然后需要根据这些信息去推导其他区间的区间和，第一眼看了是完全懵逼的，看了一位大佬的题解后【大佬贴贴】，明白可以使用带权并查集来做，这个和y总讲的算法基础课中的【食物链】这道题有点像。

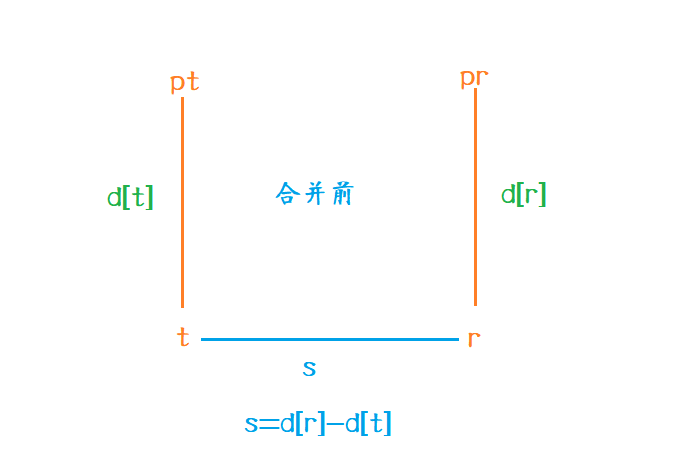
前缀和是第一个元素为参照，陆续求出后续元素的累加和，利用区间相减的原则推导出某段区间的和。使用带权并查集来做可以类比一下，我们以并查集的根节点为参照，如d[r]d[r]d[r]就表示rrr结点到所在并查集的距离，同理对于[l,r][l, r][l,r]的区间和也可以使用d[r]−d[l−1]d[r]-d[l-1]d[r]−d[l−1]来表示。假设区间[l,r][l, r][l,r]的区间和为sss，由于[l,r][l, r][l,r]区间和表示为d[r]−d[l−1]d[r]-d[l-1]d[r]−d[l−1]，也就是rrr到根的距离与l−1l-1l−1到根的距离之差，我们可以将rrr所在并查集和l−1l-1l−1所在并查集进行合并，为了方便表示不妨记录t=l−1t=l-1t=l−1。

合并前：s=d[r]−d[t]s=d[r]-d[t]s=d[r]−d[t]

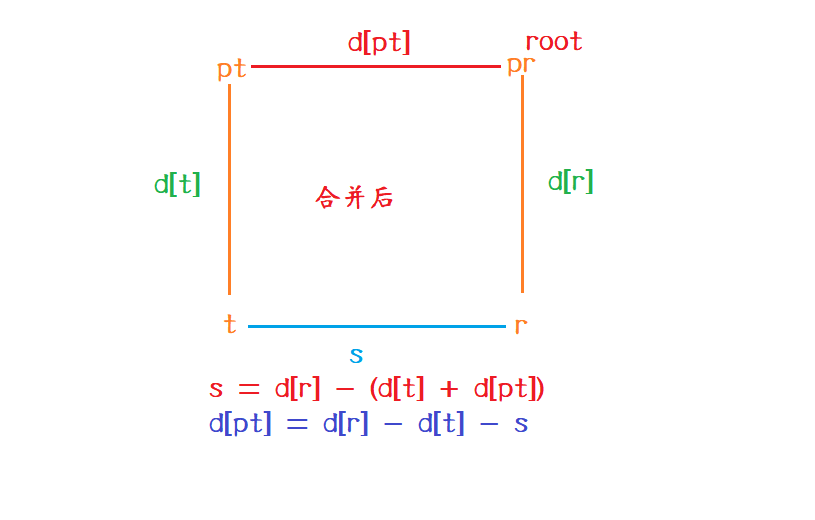
合并后：s=d[r]−(d[t]+d[pt])s = d[r] - (d[t] + d[pt])s=d[r]−(d[t]+d[pt])
d[pt]=d[r]−d[t]−sd[pt] = d[r] - d[t] - sd[pt]=d[r]−d[t]−s

将所有区间全部加入并查集后就可以直接利用类似前缀和的写法进行查询。

在查询时，如果l−1l-1l−1与rrr不在同一个并查集当中，那么肯定是求不出来了，否则可以查询到结果。

🔑源代码

并查集实现时利用路径压缩增加效率。

java 代码：

import java.util.*;class Main {static final int N = (int) 2e5 + 10;static int[] p = new int[N];static long[] d = new long[N];static Scanner sc = new Scanner(System.in);static int n, m, q;static int find(int x) {if (p[x] != x) {int t = p[x];p[x] = find(p[x]);d[x] += d[t];}   return p[x];}public static void main(String[] args) {n = sc.nextInt();m = sc.nextInt();q = sc.nextInt();//init uffor (int i = 1; i <= n; i++) p[i] = i;while (m-- > 0) {int l = sc.nextInt();int r = sc.nextInt();long s = sc.nextLong();int pt = find(l - 1), pr = find(r);p[pt] = pr;//更新d[pt]d[pt] = d[r] - s - d[l - 1];}while (q-- > 0) {int l = sc.nextInt();int r = sc.nextInt();int pt = find(l - 1), pr = find(r);if (pt != pr) System.out.println("UNKNOWN");else System.out.println(d[r] - d[l - 1]);}}
}

c++代码：

//带权并查集 与算法基础课中的食物链较像
//以一个根结点为参照，l-1到根结点的距离为d[l-1] r到根结点的距离为d[r]
//根据前缀和原理 [l, r] 区间和为 d[r] - d[l - 1]
#include 
#include 
#include using namespace std;
typedef long long LL;
const int N = (int) 2e5 + 10;//并查集 
int p[N];
//到根的权重
LL d[N];int n, m, q;int find(int x) 
{if (p[x] != x) {int t = p[x];p[x] = find(p[x]);d[x] += d[t];}return p[x];
}int main() 
{cin >> n >> m >> q;//初始化并查集for (int i = 1; i <= n; i++) p[i] = i;while (m-- > 0) {LL l, r, s;cin >> l >> r >> s;//找根结点int pl = find(l - 1), pr = find(r);//合并p[pl] = pr;d[pl] = d[r] - d[l - 1] - s;}//查询//如果l, r都在同一个集合，则存在结果，否则不能查出结果while (q-- > 0) {int l, r;cin >> l >> r;int pl = find(l - 1), pr = find(r);if (pl != pr) cout << "UNKNOWN" << endl;else cout << d[r] - d[l - 1] << endl;}return 0;
}