这几天做面试题，背包问题是一个常考的考点，我没有复习到位，都很难做出来。

很久以前我看到01背包问题的最基础那里，看完，这么简单，我会背包问题了。。。结果这几次面试题都不带重样的背包，不禁让我回来继续整理总结。非常抱歉，以下代码是我在不同时期写得，所以代码有一些是C++的有一些是java的。

1.01背包基础

https://www.acwing.com/problem/content/description/2/

这就是典型的01背包，非常简单，了解了状态定义就会写

dp[i][j]表示当容量为j的时候前i个物品的最大价值是什么？

对于初学者，建议先画表格。画了一个表格什么都明白了。

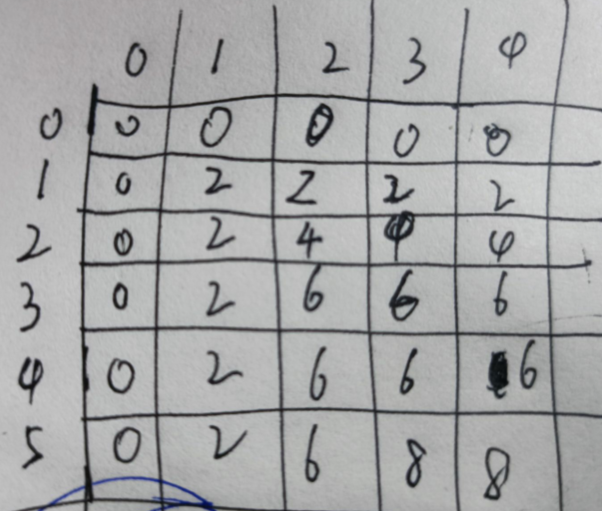
看是没有用滴，自己推理一边就知道状态方程怎么来的了。

推理方程：

dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i])

含义：不要当前的i，要当前的i。如果要当前的i的话，要看装不装的下，怎么叫装得下？j >= w[i]叫装得下.有这个思路就可以写最普通的代码了。

#include
using namespace std;
#define N 1001
int v[N];
int w[N];
int f[N][N];
int main()
{int n,m;cin >> n >> m;for(int i = 1;i <= n;i++){cin >> v[i] >> w[i];}for(int i = 1;i <= n;i++){for(int j = 0;j <= m;j++){f[i][j] = f[i - 1][j];if(v[i] <= j) f[i][j] = max(f[i][j],f[i - 1][j - v[i]] + w[i]);}}cout << f[n][m];return 0;
}

这是最常规的，那么实际上每次更新i的过程中，只用到了i - 1的状态，可以改成一维数组优化。

#include
using namespace std;
int main()
{int n, v;cin >> n >> v;int cap[n + 1] = {0};int val[n + 1]= {0};for(int i = 1; i <= n; i++) {cin >> cap[i] >> val[i];}int dp[v + 1] = {0};for(int i = 1; i <= n; i++) {for(int j = 1; j <= v; j++) {if(j - cap[i] >= 0)dp[j] = max(dp[j], dp[j - cap[i]] + val[i]);}}cout << dp[v] << endl;return 0;
}

上面的代码提供了错误的示范，j = 1, j <= v; j++，思路是没错，但是滚动的过程中，会刷新dp[j]，所以一定要从后往前滚动才可以。

#include
using namespace std;
int main()
{int n, v;cin >> n >> v;int cap[n + 1] = {0};int val[n + 1]= {0};for(int i = 1; i <= n; i++) {cin >> cap[i] >> val[i];}int dp[v + 1] = {0};for(int i = 1; i <= n; i++) {for(int j = v; j >=0; j--) {if(j - cap[i] >= 0)dp[j] = max(dp[j], dp[j - cap[i]] + val[i]);}}cout << dp[v] << endl;return 0;
}

上面的代码依然可以继续优化，如果j >= cap[i]表示买得起当前物品，否则表示买不起。买不起就不用动了，可以直接写成

for(int j = v; j >= cap[i]; j--)dp[j] = max(dp[j], dp[j - cap[i] + val[i]);

01背包的变体例题

https://www.nowcoder.com/practice/f9c6f980eeec43ef85be20755ddbeaf4?tpId=37&tqId=21239&rp=1&ru=/exam/oj/ta&qru=/exam/oj/ta&sourceUrl=%2Fexam%2Foj%2Fta%3FtpId%3D37&difficulty=undefined&judgeStatus=undefined&tags=&title=

对于上面的01背包基础还是要多多去反复品味一下，非常之妙啊，他变个形状可能就不认识了，但是一想还是01背包。

本题可以先处理一下，将每一种主键作为背包的元素，附件作为主键的状态。

import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int money = sc.nextInt() / 10;int m = sc.nextInt();int[][] w = new int[m + 1][3];int[][] v = new int[m + 1][3];int id = 1;int[][] pre = new int[m][3];Map map = new HashMap<>();for(int i = 0; i < m; i++) {int price = sc.nextInt() / 10;int imp = sc.nextInt();int states = sc.nextInt();pre[i][0] = price;pre[i][1] = imp;pre[i][2] = states;if(states == 0) {w[id][0] = price;v[id][0] = price * imp;map.put(i, id);id++;}}for(int i = 0; i < m; i++) {int states = pre[i][2];if(states == 0)continue;int price = pre[i][0];int imp = pre[i][1];int idx = map.get(states - 1);if(w[idx][1] == 0) {w[idx][1] = price;v[idx][1] = imp * price;} else {w[idx][2] = price;v[idx][2] = imp * price;}}int[] dp = new int[money + 1];for(int i = 1; i <= id; i++) {for(int j = money; j >= 1; j--) {int t = dp[j]; //不买if(j >= w[i][0]) t = Math.max(t, dp[j - w[i][0]] + v[i][0]); //买主if(j >= w[i][0] + w[i][1]) t = Math.max(t, dp[j - w[i][0] - w[i][1]] + v[i][0] + v[i][1]); //主1if(j >= w[i][0] + w[i][2]) t = Math.max(t, dp[j - w[i][0] - w[i][2]] + v[i][0] + v[i][2]); //主2if(j >= w[i][0] + w[i][1] + w[i][2]) t = Math.max(t, dp[j - w[i][0] - w[i][1] - w[i][2]] + v[i][0] + v[i][1] + v[i][2]);dp[j] = t;}}System.out.println(dp[money] * 10);}
}

完全背包问题

https://oj.youdao.com/problem/725

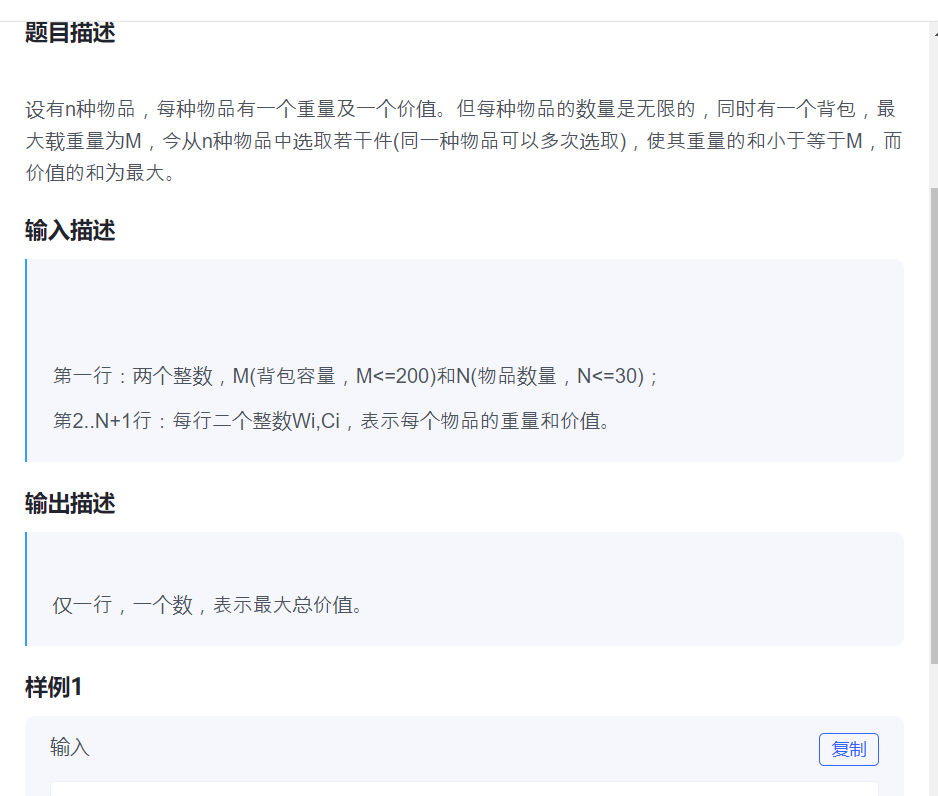
如题所示，完全背包问题和01背包问题的差别在于：完全背包问题是可以重复出现多次的。

#include
using namespace std;
int main()
{int m, n;cin >> m >> n;int w[n + 1] = {0};int v[n + 1] = {0};int dp[m + 1] = {0};for(int i = 1; i <= n; i++) {cin >> w[i] >> v[i];}for(int i = 1; i <= n; i++) {for(int j = w[i]; j <= m; j++) {dp[j] = max(dp[j], dp[j - w[i]] + v[i]);}}cout << "max=" << dp[m] << endl;return 0;
}

如果熟悉了上面的01背包，再看这个应该很简单，如果买不起当前的，很显然就不买。

否则dp[j - w[i]]+ v[i]

https://leetcode.cn/problems/coin-change-ii/

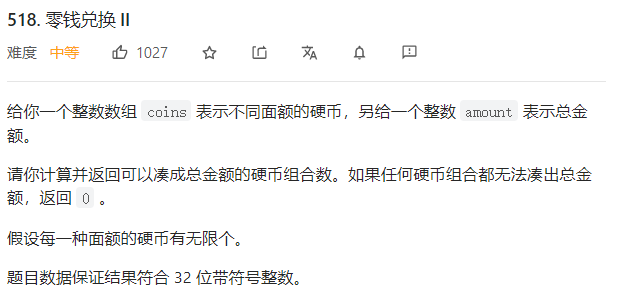
这也是个完全背包问题。。。如果不告诉我，我真的联想不到，可能脑子不好使吧。

class Solution {
public:int change(int amount, vector& coins) {vector dp(amount + 1);dp[0] = 1;for(int t: coins) {for(int i = t; i <= amount; i++) {dp[i] += dp[i - t];}}return dp[amount];}
};

https://leetcode.cn/problems/coin-change/

零钱兑换问题1，也可以看作是一个完全背包问题。

int coinChange(vector& coins, int amount) {vector dp(amount + 1, 10000000);dp[0] = 0;for(int coin: coins) {if(coin > amount) continue;dp[coin] = 1;for(int j = coin + 1; j <= amount; j++) {dp[j] = min(dp[j - coin] + 1, dp[j]);}print(dp);}return dp[amount] == 10000000 ? -1 : dp[amount];}
int print(vector &dp) {for(int d: dp)cout << d << " ";cout << endl;return 0;}

这里我打印了一个case看看

0 1 2 3 4 5 6 7 8 9 10 11 
0 1 1 2 2 3 3 4 4 5 5 6 
0 1 1 2 2 1 2 2 3 3 2 3 

https://leetcode.cn/problems/combination-sum-iv/

组合总和问题：这里又变了一下，我又没想到。。。

class Solution {
public:int combinationSum4(vector& nums, int target) {vector dp(target + 1);dp[0] = 1;for(int i = 1; i <= target; i++) {for(int n: nums) {if(i >= n && dp[i] < INT_MAX - dp[i - n]) dp[i] += dp[i - n];}}return dp[target];}
};