鲁政委、顾怀宇、王宏、黄之豪（鲁政委系兴业银行首席经济学家、中国首席经济学家论坛理事）

大类资产配置，BL模型，风险平价

引言：在低利率环境下，如何平衡风险与收益、科学配置大类资产，已成为资管及自营机构关注的核心议题；同时，如何有效融合主观观点、发挥研究优势，也成为其迫切探索的方向。

资产配置模型的演进可划分为四个阶段：以均值-方差（MVO）模型为代表的现代投资组合理论；以Black-Litterman（BL）模型为核心的主观观点融合阶段；以风险平价（Risk Parity）为标志的风险再平衡阶段；以及以因子投资为主导的收益解构阶段。

在资产配置模型的机构适配方面，均值方差模型对预期收益和协方差的估计极为敏感，适用于研究实力强、能形成明确主观观点的机构；在国际实践中，海外较少直接用MVO，仅作为战略研究模型工具。固定权重模型则呈现出更强的实践导向：广义60/40组合优势在于透明、易执行，且在长期历史中表现稳健，能够作为许多养老金和年金资金的核心框架，但其在股债同跌的极端市场中往往面临较大回撤。进一步分散的永久投资组合与等权配置对经济周期具有较强的适应性，回撤控制较好，但缺点在于在权益牛市阶段明显跑输股市，长期超额有限。

风险平价模型优点在于能够显著降低单一资产对组合的冲击，提高夏普比率，并在历史上展现出稳健的回撤控制能力。然而，该方法未显式纳入收益率预期，如果某一时期某类资产的预期收益偏低，风险平价仍可能给予其较高权重，从而导致潜在的机会成本。基于这些特点，风险平价更适合：1）追求稳健的养老金、银行理财子公司；2）具备较强单一资产超额获取能力的量化私募；3）缺乏预测能力的个人投资者；4）资金体量庞大、不支持高频择时的机构（如社保基金、养老金）。

Black-Litterman（BL）模型核心价值更体现在作为“观点嵌入框架”的灵活性上，本文研究表明，当主观预测胜率达到60%–65%及以上时，在BL模型中嵌入部分核心资产的观点，能够有效提升收益。同时，BL模型可与均值方差、风险平价等多种模型结合。相较于风险平价模型直接通过类线性方式调整风险权重，BL模型基于贝叶斯方法融合主观观点更为稳健。但BL模型的挑战在于依赖观点预测的准确性，同时参数设定较复杂，该方法适合理财子公司、资管机构、FOF/MOM管理人等需要在均衡配置基础上叠加行业或主题观点的机构。

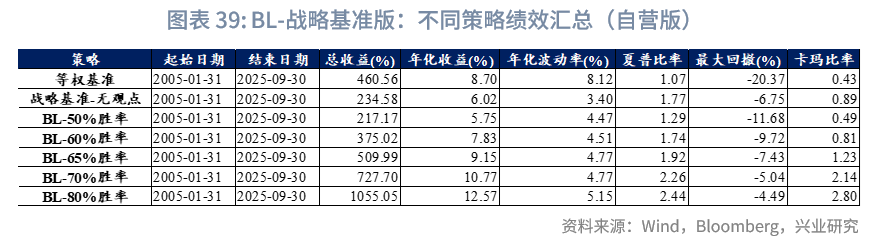
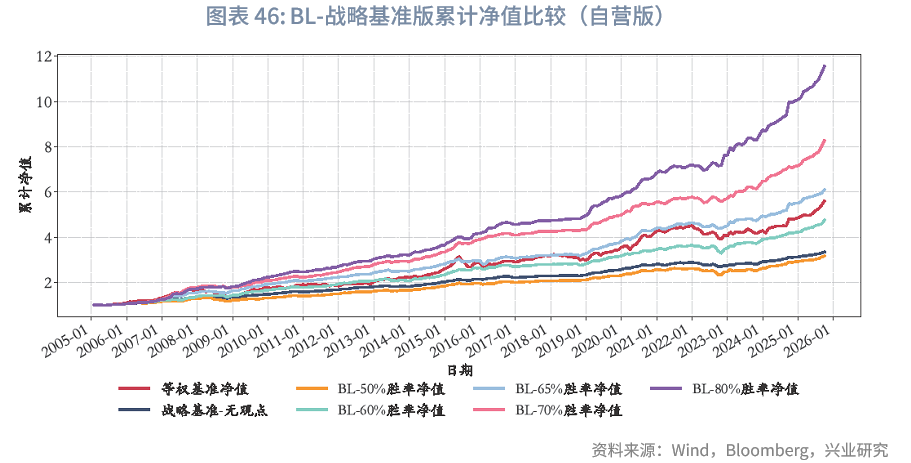
无观点版本下，风险平价-无观点版夏普比率最高，BL-战略基准-自营-无观点版回撤最小；均值方差、股50债40黄金10年化收益率最高。样本期为2005年至今的样本期内，各模型在收益表现和风险收益比方面的表现如下：年化收益率方面，均值方差（10.61%）＞股50债40黄金10（8.80%）>等权组合（8.70%）＞BL-战略基准-资管-无观点版（8.10%）＞永久组合（8.00%）＞风险平价-无观点版（6.39%）>BL-战略基准-自营-无观点版（6.02%）。夏普比率方面，风险平价-无观点版（1.83）＞BL-战略基准-自营-无观点版（1.77）＞BL-战略基准-资管-无观点版（1.26）＞永久组合（1.20）＞股50债40黄金10（1.08）＞等权组合（1.07）＞均值方差（0.65）。

有观点版本下（65%主观胜率），风险平价-65%胜率夏普比率最高、回撤最小；BL-战略基准-资管-65%胜率年化收益率最高。在样本期为2005年至今的样本期内，各模型在收益表现和风险收益比方面的表现如下：年化收益率方面，BL-战略基准-资管-65%胜率（11.34%）＞BL-战略基准-自营-65%胜率（9.15%）＞BL-风险平价-65%胜率（8.13%）＞风险平价-65%胜率（7.94%）。夏普比率方面，风险平价-65%胜率（2.36）＞BL-风险平价-65%胜率（1.93）＞BL-战略基准-自营-65%胜率（1.92）＞BL-战略基准-资管-65%胜率（1.51）。

基于历史回测结果，针对不同机构，提供以下建议：无主观观点时，保守型机构推荐BL-战略基准-自营模型（无观点版）或风险平价模型，收益风险平衡型机构推荐BL-战略基准-资管机构模型或股50债40黄金10；机构研究实力强且核心资产长期预测胜率超60~65%时，推荐主观观点版，含主观观点的模型较无观点模型，年化收益率提升约2%以上、最大回撤减少1%以上、夏普比率提升0.2以上。

大类资产配置（Asset Allocation）被认为是投资决策中最重要的环节，它旨在通过在不同资产类别（如股票、债券、商品等）之间分配资金，以在给定的风险承受能力下最大化长期回报，或为实现特定回报目标而最小化风险。学术界和业界普遍认为，长期来看，超过90%的投资组合回报波动源于资产配置决策(Brinson et al., 1986; Hood R L, 2005)。因此，构建科学、稳健的资产配置模型一直是金融学研究的核心课题之一。

一、大类资产配置方法综述

资产配置模型的演化历程大致可划分为四个核心阶段：第一阶段以现代投资组合理论的诞生为标志，核心模型为均值- 方差模型（Mean-Variance Model）；第二阶段聚焦主观判断的融入，以 Black-Litterman 模型为代表性成果；第三阶段转向对风险的重新审视，风险平价模型（Risk Parity Model）成为该阶段的关键实践方向；第四阶段则以资产收益的解构为核心逻辑，因子投资（Factor Investing）逐步发展为主流范式。

第一阶段：现代投资组合理论的诞生——均值-方差模型 (Mean-Variance Model)

大类资产配置的量化发展进程以1952年为关键起点，诺贝尔经济学奖得主哈里·马科维茨（Harry Markowitz）在该年发表的开创性论文《投资组合选择》（Portfolio Selection）中，首次系统性构建了现代投资组合理论（Modern Portfolio Theory, MPT）的核心框架（Markowitz, 1952）。这一理论突破的核心在于，马科维茨摒弃了传统投资分析中对资产收益与风险的定性描述，转而提出以资产收益的均值（即期望收益）作为回报水平的客观度量指标，以收益的方差（或标准差）作为风险的可量化工具，为资产配置的科学化分析奠定了方法论基础。

均值-方差模型（Mean-Variance Optimization, MVO）作为MPT的核心分析工具，其理论逻辑建立在“理性投资者具有风险厌恶特征”的基本假设之上：该类投资者的核心目标是在给定风险水平下实现收益最大化，或在预设收益目标下实现风险最小化。通过对不同风险收益特征资产的组合优化，可筛选出一系列满足上述最优条件的投资组合，这些组合在风险-收益二维坐标系中形成的连续集合被定义为“有效前沿”（Efficient Frontier）——所有位于有效前沿下方的投资组合，均因无法实现风险与收益的最优匹配而被归为次优组合。MVO模型的诞生具有里程碑意义，它标志着投资决策领域从传统依赖经验判断与主观偏好的“艺术化”阶段，正式迈向以数据驱动、模型计算为核心的“科学化、量化化”新阶段，彻底重塑了资产配置的分析范式。

自MVO模型提出后，学术界与实务界围绕有效前沿的理论拓展与实践适配展开了持续探索。在理论深化层面，Broadie（1993）聚焦有效前沿估计过程中的核心矛盾，通过实证分析系统揭示了估计误差与估计结果平稳性之间的权衡关系，为后续模型估计方法的改进提供了关键理论参考；在算法优化层面，Woodside-Oriakhiet al.（2011）针对传统优化算法在处理复杂约束时的局限性，将遗传算法、禁忌搜索及模拟退火等元启发式算法引入金融投资组合优化领域，重点验证了此类算法在求解带基数约束（即限制组合中资产数量）的有效前沿问题中的可行性与效率优势；在领域拓展层面，随着环境、社会与治理（ESG）投资理念的兴起，Pedersenet al.（2021）进一步将有效前沿理论与ESG投资目标相结合，构建了融合ESG绩效指标的有效前沿分析框架，为负责任投资的组合优化提供了适配性理论支撑，推动有效前沿的应用场景从传统金融领域延伸至可持续投资领域。

尽管MVO模型是现代资产配置的重要理论基石，但其实际应用中存在显著局限，对输入参数的高度敏感性尤为业界诟病。Bestet al.（1991）实证证实，当MVO施加资产权重非负约束（禁止卖空）时，正加权MVO有效组合的权重对资产期望收益（均值）的微小变动高度敏感，而组合整体收益却无显著波动。实践中，单一资产期望收益小幅上调即可能导致组合近半数证券被调出，引发剧烈权重重构；此类“参数微变致配置大幅偏离”的特征，既增加组合管理难度，也削弱了MVO的实际应用稳定性与可靠性。虽有学者尝试改进，如Alexander et al. (2002)将风险价值（VaR）与传统MVO结合，试图解决其风险衡量对称、分布假设过严及效用支撑薄弱的缺陷，但整体改进效果有限，而且均值方差组合样本外表现要超越等权组合的时间过长(Broadie, 1993)，致使MVO至今在业界应用较少。

第二阶段：融入主观判断——Black-Litterman模型

为了解决均值-方差模型对输入参数过于敏感且不稳定的问题，高盛公司的研究员费希尔·布莱克（Fischer Black）和罗伯特·利特曼（Robert Litterman）在20世纪90年代初开发了Black-Litterman（BL）模型，其标志性学术论文《全球投资组合优化》（Global Portfolio Optimisation）于1992年正式发表于《金融分析师杂志》（Black & Litterman, 1992）。

BL模型基于贝叶斯方法，核心是整合两类关键信息以优化预期收益输入：一是市场均衡收益（先验信息），无需投资者直接预测资产绝对收益，而是通过全球市场组合权重反推隐含的市场均衡收益率，作为市场共识的中性基准；二是投资者主观观点（最大似然），提供结构化框架允许投资者以绝对或相对形式表达对资产未来表现的前瞻性判断，并明确观点的信心水平。两类信息经贝叶斯整合后生成综合预期收益向量（后验收益），作为MVO模型输入进行组合优化，最终输出的权重通常更稳定、分散且契合投资直觉。

在国内实践中，学者对BL模型主观观点的构建方式已形成多元路径：以绝对观点为主流，常见如直接采用技术分析、情绪指标、历史交易数据（宋正阳等）或AdaBoost集成算法预测的资产期望超额收益（姚海祥等, 2023）作为观点；亦有研究将股吧观点等情绪指标映射为投资者主观观点（孟勇等, 2022；庞杰, 2021）；此外，通过划分经济周期，计算不同周期下各类资产的超额收益以形成观点，也是广泛应用的思路（王莹等, 2022；周亮, 2021；周亮等, 2019, 2020）。

BL模型的核心优势在于搭建了量化模型与基金经理主观能动性的衔接桥梁：既依托市场集体智慧（均衡收益），又为专业投研判断（主观观点）提供落地场景。因此，该模型自诞生后便被高盛资管部门广泛应用，并迅速推广至全球养老金（乌云高, 2022）、主权财富基金及资产管理公司，成为机构资产配置的标准工具之一。但其局限性亦十分显著：最终配置效果高度依赖投资者主观观点的质量与准确性。

第三阶段：风险的重新审视——风险平价模型 (Risk Parity Model)

当均值-方差和BL模型仍受困于收益预测的不确定性时，一种全新的范式开始兴起，它将关注的焦点从“收益最大化”转向了“风险均衡化”。这就是风险平价（Risk Parity）模型。虽然其思想渊源可以追溯更早，但真正将其发扬光大并成功商业化的是桥水基金（Bridgewater Associates）创始人瑞·达利欧（Ray Dalio）及其在20世纪90年代推出的“全天候”（All Weather）策略。学术界中，Qian（2011）及 Qian et al.（2005）的研究也为该模型的理论发展做出了重要贡献。

风险平价模型的核心逻辑在于：真正的分散化投资组合需实现风险层面的均衡分配，而非仅关注资金权重的分散。该模型主张在组合构建中，使各资产类别对组合总风险的贡献度保持一致。以传统60/40股债组合为例，股票虽仅占60%的资金权重，对组合总风险的贡献却常超90%；而风险平价策略通过降低高风险资产（如股票）的配置比例、提高低风险资产（如债券）的配置权重，并借助杠杆工具将低风险资产的预期收益提升至目标水平，最终实现不同资产间的风险均衡分配。

从实践定位来看，风险平价策略旨在构建能够抵御增长、衰退、通胀、通缩等不同经济环境冲击的稳健组合，其追求长期稳健回报、降低下行风险的特性，使其受到众多大型长期投资者（尤其是养老基金）的青睐。例如，丹麦最大养老基金ATP便是风险平价策略的典型实践者，其将风险预算均匀分配至股票、利率、通胀、信用等不同风险因子；国内研究中，林雷等（2025）围绕养老金入市收益展开测算，王玉国（2018）则对比风险平价与传统60/40模型，发现风险平价模型表现更优——在收益水平基本相当的情况下，其波动性仅为传统策略的1/5左右，夏普比率则达传统策略的4.7倍；国外学者Asness et al.（2012）亦得出类似结论，其研究表明，借助杠杆的风险平价组合可实现与市场组合相当的风险水平，同时获得更高的预期收益。

不过，风险平价策略并非无懈可击。该策略对杠杆的依赖使其面临额外的融资风险与流动性风险，且在股票市场长期牛市环境中，其业绩表现可能落后于传统偏股型组合，这也构成了其应用场景中的核心局限。

第四阶段：解构资产收益——因子投资 (Factor Investing)

进入21世纪，资产配置理论前沿进一步深化，其核心演进方向表现为从传统的“资产类别导向”转向“风险因子驱动”——即聚焦于解释资产回报的共性风险因子（Risk Factors），这一范式被定义为因子投资。该范式的理论基石可追溯至Fama与French（1992）提出的三因子模型，该模型突破传统市场风险单一视角，指出市值（Size）与账面市值比（Value）同样是解释股票超额回报的关键变量。

因子投资的核心逻辑在于：任何资产类别的回报均可解构为其对一系列系统性风险因子的暴露程度。据此，资产配置的本质并非对股票、债券等表层资产的选择，而是对增长、通胀、价值、动量等底层风险因子的战略性配置（Dichtl et al., 2021）。通过直接锚定此类因子进行配置，投资者既能更精准地构建目标风险暴露，实现比传统资产配置更优的分散化效果，亦有望通过捕获因子风险溢价获取超额收益。值得注意的是，Smart Beta 理念同样源于三因子模型，周静（2024）通过构建基本面组合、等权组合、分散化最小方差组合及分散化风险平价组合，采用基于多项式目标规划的均值-协方差-协偏矩组合策略（PGP-MVS）框架进行动态加权，最终实现了显著的超额收益。

因子投资为解析投资组合收益来源提供了更深刻、更本质的分析视角，目前已被众多成熟机构投资者及主权财富基金广泛采纳。在实践策略层面，部分学者指出因子择时难度较大，认为在不同因子间开展战略性分散投资通常比主动择时尝试更有效，Asness（2016）等亦持类似观点。在因子分类领域，现有研究呈现多元视角：宏观因子层面，常见类别包括经济增长、实际利率、通胀、信贷、新兴市场及大宗商品等；Vanguard（先锋领航）则将因子划分为市场因子、价值因子、规模因子、动量因子、低波动因子、期限因子及信用因子七大类（Pappas et al., 2015）；另有学者从资产类别维度拆分因子，如股票因子（盈利收益率、滞后价格动量）、债券相关因子（期限结构、实际利率）及货币因子（与美元利差）（Clarke et al., 2005）。从实证证据看，Bass et al.（2017）的研究发现，经济增长因素在全球公开股票与全球私募股权的总风险中占比均超 50%，且私募股权对经济增长的敞口更大；而全球总债券则主要受实际利率、通胀及信贷因素影响，其中对信贷因素的敞口最小。

尽管因子投资应用广泛，但其发展仍面临显著挑战：一方面，学术界与业界对“何为真正稳健的风险因子”尚未形成统一共识，即存在所谓的 “因子动物园”（factor zoo）问题(Cochrane J H, 2011)；另一方面，各类因子具有内在周期性特征，可能面临长期表现低迷的阶段。

新的前沿：机器学习、动态配置与未来展望

随着算力的提升和大数据技术的发展，大类资产配置正迈入一个新的前沿。机器学习（Machine Learning）和人工智能（AI）方法，如强化学习、深度学习神经网络、大语言模型等，开始被应用于资产配置领域。这类模型的核心优势在于，能够从海量、多维度的传统金融数据与另类数据中，有效学习并识别复杂的非线性关系及动态演变的市场范式，其最终目标是构建具备自适应调整能力的动态资产配置策略，以应对日益复杂且快速变化的市场环境。

当前该领域的前沿探索主要聚焦于三大方向：新兴资产类别拓展、非结构化数据应用深化及智能交易代理构建。在新兴资产应用层面，部分学者已尝试将ML 方法引入加密货币风险管理领域，通过模型优化实现风险识别与控制（Burggraf，2021）；另有研究将 LLMs 应用于加密货币大类资产配置管理，为该类资产的配置提供新的技术路径（Luo et al.，2025）。在非结构化数据与 LLM 的融合应用中，Ko et al.（2024）以 ChatGPT 为研究对象，探索其在多资产类别选择中的有效性，并通过实证评估其配置的分散化效果，结果表明，ChatGPT 所选资产在多样性指数层面显著优于随机资产选择。在智能交易代理构建方面， AI Hedge Fund(2025) 项目提出“多策略代理”框架，将 AI 代理设计为不同投资策略的模拟器，每个代理对应一种经典投资哲学或策略（如本杰明・格雷厄姆价值投资代理、查理・芒格多元思维代理、技术分析代理等），通过 AI 与数据分析的协同实现市场化决策；Li et al.（2025）则进一步基于GPT-4o Mini等轻量级模型开展全面微调，构建“LLM-传统量化”混合交易模型，实证结果显示，该模型在预测准确性与风险调整后收益两方面均实现显著提升。

从应用现状来看，当前此类前沿方法的落地仍集中于少数顶尖量化对冲基金，其应用场景主要聚焦于战术资产配置与高频交易策略。然而，受限于三大核心挑战，其在长期机构资产配置中的应用仍处于探索阶段：一是ML/AI 模型普遍存在的“黑箱”特性，难以满足机构配置对决策透明度的要求；二是模型对高质量数据的高度依赖，数据可得性与完整性直接制约其适用性；三是模型过拟合风险显著，可能导致策略在极端市场环境下失效，而长期机构资产配置恰恰对透明度与稳健性存在刚性需求。

二、大类资产配置方法原理

本文重点对比均值方差（MVO）模型、Black-Litterman（BL）模型、风险评价模型、永久组合及广义60/40模型。研究中，针对风险平价模型与BL模型，引入基于胜率的主观观点开展测试；同时将BL模型与风险平价模型进行组合，构建出基于胜率的BL-风险平价模型。

2.1.1 均值方差（MVO）模型

均值方差模型（Mean-Variance Model）是现代投资组合理论（Modern Portfolio Theory，MPT）的核心框架，由美国经济学家哈里·马科维茨（Harry Markowitz）于1952年在《金融杂志》发表的《大类资产配置的选择》一文中提出。该模型首次将“收益”与“风险”进行量化，解决了“如何在给定风险水平下最大化收益，或在给定收益水平下最小化风险”的投资组合优化问题，为现代资产管理奠定了理论基础。

模型原理：

2.1.2 广义60/40组合

在资产配置实践中，固定权重策略因其结构透明、执行简便、历史表现稳健，被广泛应用于养老金、保险资金、财富管理及FOF/MOM等中长期投资场景。本报告基于后文实际回测框架，介绍以下三种主流固定权重配置模型：

股60债40组合：经典增长型配置

债60股40组合：保守稳健型配置

股50债40黄金10组合：抗通胀增强型配置

以“股60债40组合”为例（其他两种配置方案仅调整大类资产的权重占比），该配置模型设定的资产结构为：权益类资产占比60%，固定收益类资产占比40%。

2.1.3 永久投资组合

Harry Browne 原版永久投资组合（Permanent Portfolio）是20世纪最具影响力的被动投资策略之一，由美国投资大师、作家、政治家 Harry Browne 于1980年代系统提出。其核心理念是：“不预测、不择时、不博弈——通过四类资产各占25%，构建一个无论经济处于繁荣、衰退、通胀或通缩都能保值增值的‘永久性’投资组合。”该策略以极简结构、超低维护、穿越周期著称。

需要指出的是，60/40组合与永久投资组合并非期初完成资产配置后便持仓不动，而是遵循固定权重规则：例如某月度若某一资产出现超涨，这两类组合均会对该资产进行减配操作，从本质上看，这一调整逻辑也属于一种“再平衡”方案。

2.1.4 风险平价模型

传统投资组合（如60/40股债组合）中，股票往往贡献超90%的组合波动，导致风险高度集中于单一资产。风险平价（Risk Parity）作为一种资产配置策略，核心是通过调整资产权重，让组合中每个资产（或资产类别）对整体风险的贡献相等——这区别于传统均值-方差模型按资本权重分配的逻辑，能实现真正的风险分散。该模型由桥水基金（Bridgewater Associates）在“全天候策略”中广泛应用，旨在达成更稳健、分散化的风险收益特征。

2.1.5 Black-Litterman（BL）模型

Black-Litterman（BL）模型是一种在资产配置中广泛应用的贝叶斯组合优化模型，由Fischer Black与Robert Litterman于1990年代初在高盛公司任职期间提出，其核心思想在于通过贝叶斯框架将市场均衡隐含收益（作为先验分布）与投资者主观观点（作为似然函数）进行系统性融合，从而生成稳健的后验预期收益估计，以克服传统均值-方差优化模型对输入收益高度敏感所导致的组合极端化与不稳定性问题；该模型不仅尊重市场整体结构所蕴含的信息，还允许投资者以结构化方式（如相对或绝对收益观点及其置信水平）注入主动判断，最终输出兼具市场中性与观点驱动特性的优化资产配置，在全球养老基金、主权财富基金及多资产量化策略中被广泛采用，成为现代投资组合理论从理论走向实践的重要桥梁。

三、大类资产配置的经验实证比较：基于当前国内机构

3.1.1 资产池选择与样本期

（1）资产池选择

本文将大类资产划分为现金、固定收益、权益及类权益、商品四大类别，资产池的构建遵循两大核心要点：（1）主要立足国内银行视角，例如国际上通常以1-3年美债指数代表现金类资产，本文则选用国内货基指数，且始终将固定收益类资产作为核心底仓；（2）充分考虑权益类产品的落地可行性，例如，MSCI新兴市场股票指数涵盖中国、越南、印度等多个市场的股票，在大类资产配置中更能发挥分散配置的价值，但国内并没有相关ETF产品，故选择恒生科技指数作为替代。

基于上述原则，最终初步选定18个子类资产，具体包括：（1）现金类：货基指数；（2）固定收益类：涵盖美债长久期、美债高收益、美债投资级、中债长久期、中国高收益、欧债、德债；（3）权益及类权益类：包含创业板、红利、恒生科技、美国科技、美国大盘、日本股票、德国股票、中国REITs、中国可转债；（4）商品：黄金。

需补充说明的是，对于欧债，ICE Euro Government Bond Index (All Maturities)虽为市场常用指数，但受限于数据可得性，本文选用彭博相关指数作为替代；而REITs因兼具基础设施与房地产属性，部分研究中将其归为另类投资，本文则参考证监会分类标准，将其纳入类权益产品范畴。

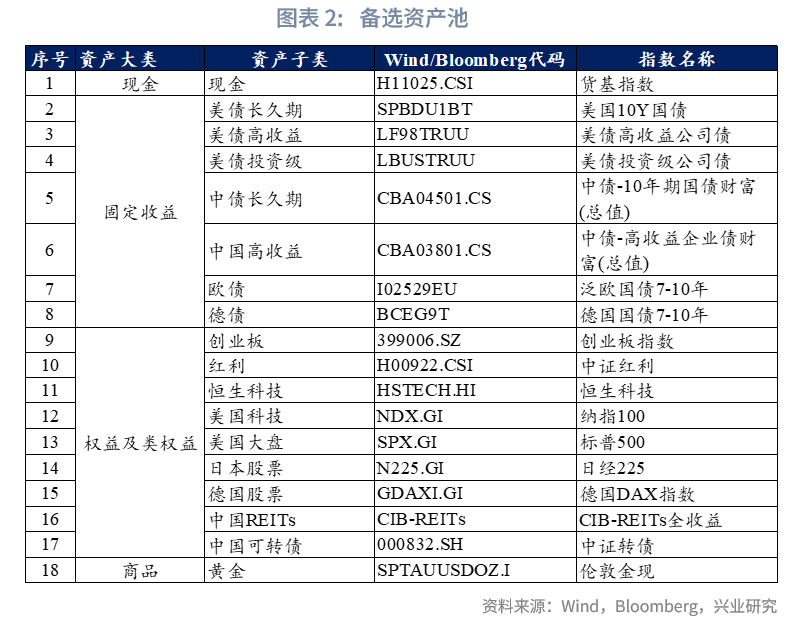
考虑到不同资产间可能存在较高相关性（从大类资产配置视角看具备较强替代性），因此本文在进入具体配置模型前，先通过相关性矩阵分析对上述初步确定的18类大类资产开展二次筛选，保留低相关资产，筛选结果如下：（1）在美国10年期国债与美债投资级两类资产中，最终选定美国10年期国债。二者相关系数达0.98，且美国10年期国债通常充当市场利率标杆，跟踪该资产的基金产品更为丰富，因此确定保留美国10年期国债指数；（2）纳指100与标普500指数的相关性为0.96，其中纳指100更能反映全球科技行业发展趋势，故本文选择纳指100作为配置标的，但在具体实践场景下，二者也可实现相互替代；（3）德债7-10年指数与泛欧国债7-10年指数的相关性达0.96，考虑到泛欧国债涵盖法国、意大利等多国国债，覆盖范围更广泛，本文选择泛欧国债7-10年指数；（4）日经225与德国DAX指数均代表非美发达国家资本市场，从与其余资产的相关性角度考量，日经225具备更强的分散配置价值，因此本文选定该指数。经上述筛选剔除后，最终剩余14个资产子类，分别为：现金、美国10年期国债、美债高收益、中国10年期国债、中债高收益、泛欧国债7-10年、创业板、中证红利、恒生科技、纳指100、日经225、中证转债、中国REITs、伦敦金现。

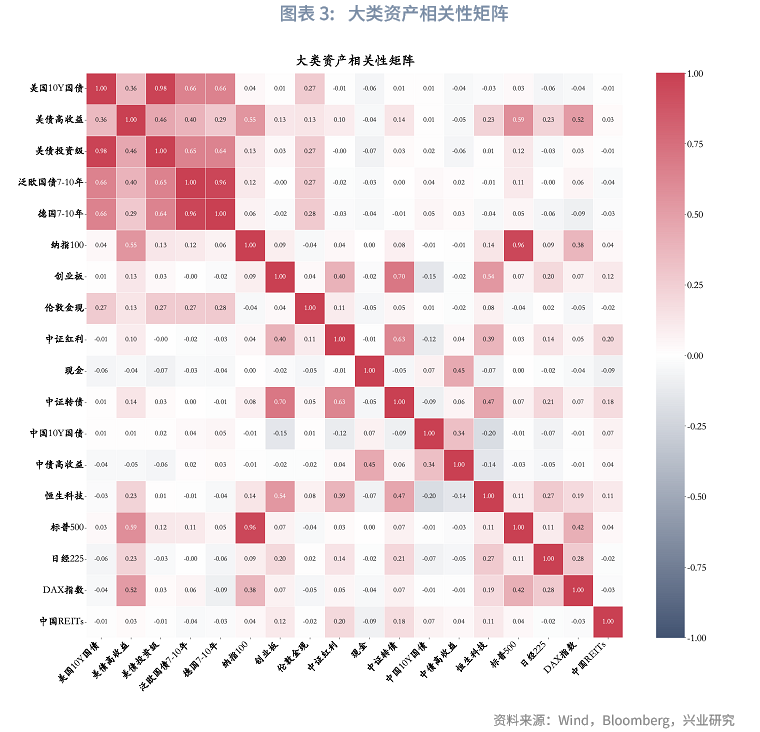
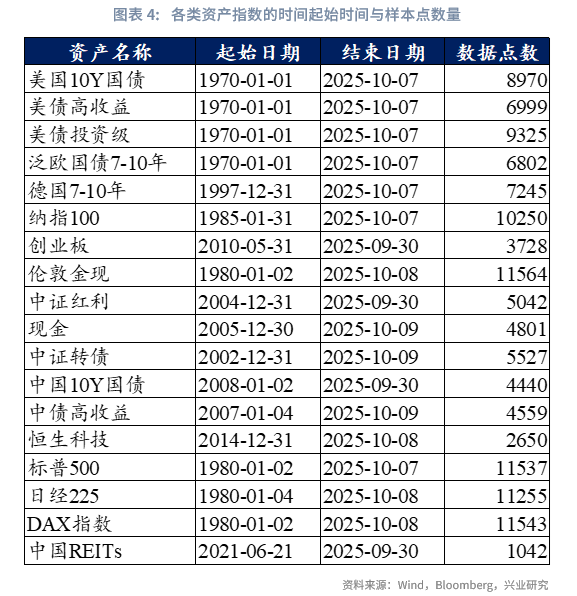
（2）样本期和权重调整日

各类资产指数的起始时间与样本点数量如下表所示。考虑到多数指数的起始时间特征，若未特别说明，本文研究样本期统一设定为2005年1月1日至2025年9月30日。所有资产权重调整以当月月末为时间节点，即于当月月末确定下一个月的资产配置权重；同时，鉴于各指数起始时间存在差异，每月将先筛选确定有效资产池（仅纳入当期已有完整数据的资产），再开展后续配置操作。

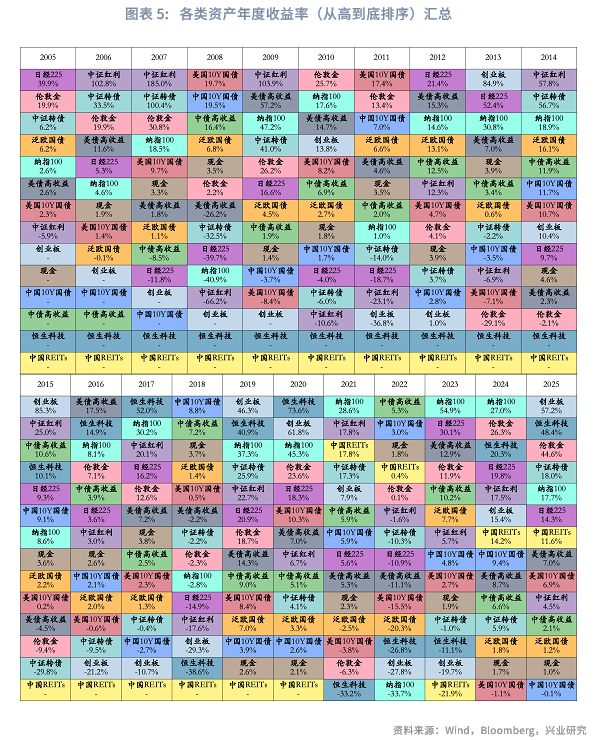
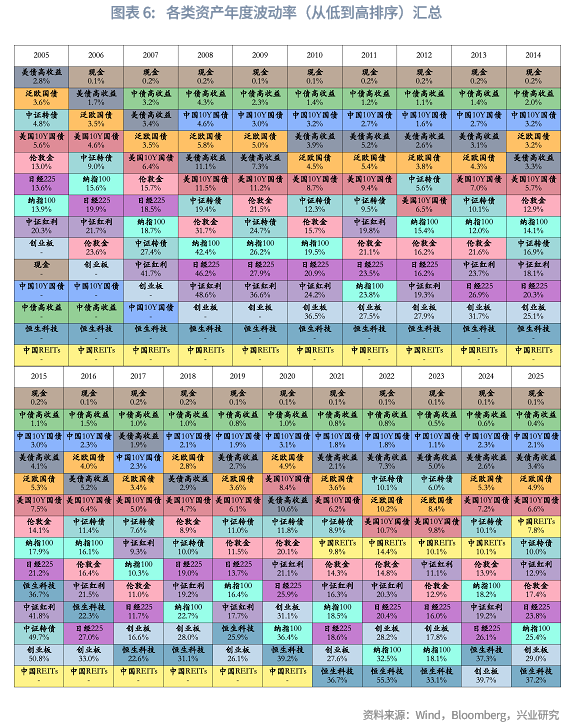
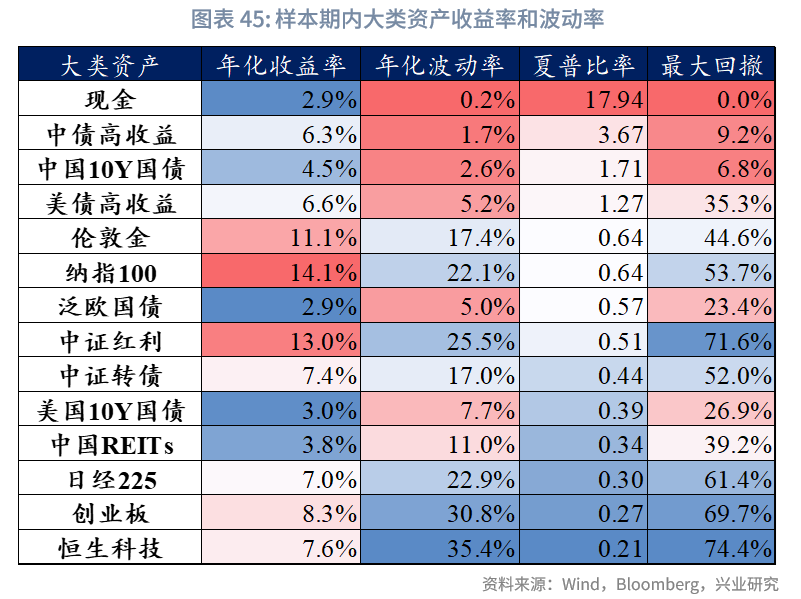
（4）各类资产收益率与波动率

下面两个表展示了筛选后的14个资产子类在样本期内各年度的收益率与波动率情况（样本期内整体年化收益率、年化波动率、夏普比率见附录）。统计分析表明以下几点：（1）现金（货币基金）收益率排名靠前的年份（如2008年、2018年及2022年），通常对应大类资产配置难度较高的市场环境。该类资产表现突出，往往意味着其他大部分资产难以提供正收益，甚至多数出现负收益，从而突显其避险属性；（2）在上述市场环境复杂的年份中，中国10年期国债与中债高收益债券普遍表现优异，基本位列当年收益率前两位。

3.1.2 均值方差模型

均值方差模型实践角度仍存在多个缺陷。首先，该模型对输入参数（尤其是资产预期收益率和协方差矩阵）高度敏感。在实际应用中，这些参数通常基于历史数据估计，而历史表现未必能准确预测未来，导致模型输出的最优投资组合可能严重偏离真实最优解。此外，模型在优化过程中往往产生高度集中或不稳定的资产配置结果。例如，微小的参数扰动可能导致权重在不同资产间剧烈跳变，这种“组合不稳定性”使得实际投资难以执行，也增加了交易成本。

本文采用滚动4年的历史数据计算资产的预期收益率与协方差矩阵，而对大多数资产而言，4年时长已足以形成一个小周期。我们设计了两个版本的均值方差模型：（1）均值方差-无仓位限制版本（作为基准版本）：不设置单个资产的仓位上限；（2）均值方差-单资产30%限制版本：在无仓位限制版本的基础上，增设单个资产30%的权重上限。同时，将等权配置模型作为参照模型，用于与上述两个均值方差模型版本进行对比分析。

组合权重方面，均值方差模型往往倾向于将权重集中投向组合内的少数几类资产，导致其余资产权重极低，同时其仓位呈现出较强的动量属性。从样本期内各资产的平均仓位来看，纳指100以18.6%的占比位列第一，其后依次为中证红利、伦敦金、中债高收益及创业板；上述六类资产的平均仓位总和约为76.9%。

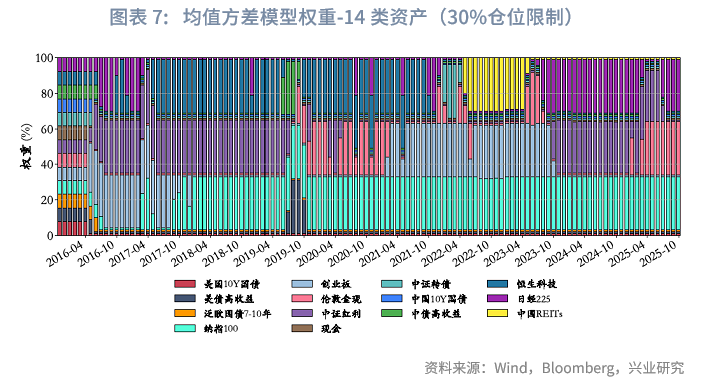
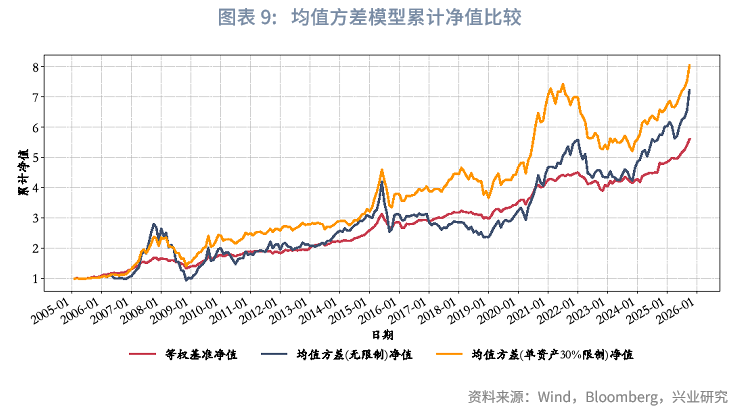
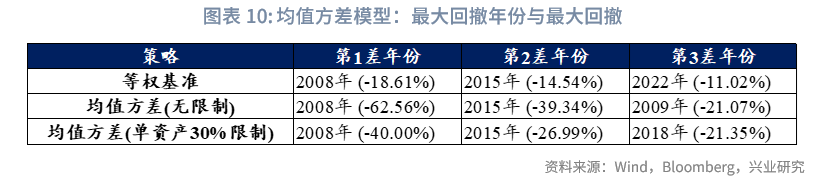
风险收益方面，样本期内，均值方差模型在实际应用中表现出稳定性不足、风险调整后收益偏低的问题。具体来看，未施加任何持仓限制的均值方差策略虽实现年化收益率10.05%，但年化波动率高达23.69%（显著高于等权基准的8.12%），夏普比率仅为0.42，最大回撤达66.35%，卡玛比率仅0.15，反映出其在承担较高波动与下行风险的同时，未能获得与之匹配的风险溢价；相比之下，引入单资产持仓不超过30%限制的均值方差策略表现更为稳健，年化收益率提升至10.61%，同时年化波动率下降至16.25%，最大回撤收窄至40.69%，但结合前文平均仓位分析可知，该模型大量仓位集中于权益或类权益资产，实际组合收益却未体现出高收益特征，其夏普比率和卡玛比率也仅分别改善至0.65和0.26，整体而言，均值方差模型在无约束条件下易产生过度集中、高波动的配置结果，导致组合稳定性较差、性价比偏低；而通过设置合理的单资产限额，虽能在一定程度上缓解此类问题，但组合仍不具备理想性价比。

3.1.3 Black-Litterman-战略基准模型

（1）战略基准权重（Wmkt）设置

本文在第二部分BL模型推导部分已指出，市场隐含均衡收益在实践中可通过战略基准或风险平价模型给出的权重进行替代，这两种方式也更贴合实际应用场景，因此本文先对战略基准版本的BL模型（下称“BL-战略基准版”）开展回测。具体而言，回测过程中重点考虑两类应用主体：一是资管机构，二是自营。

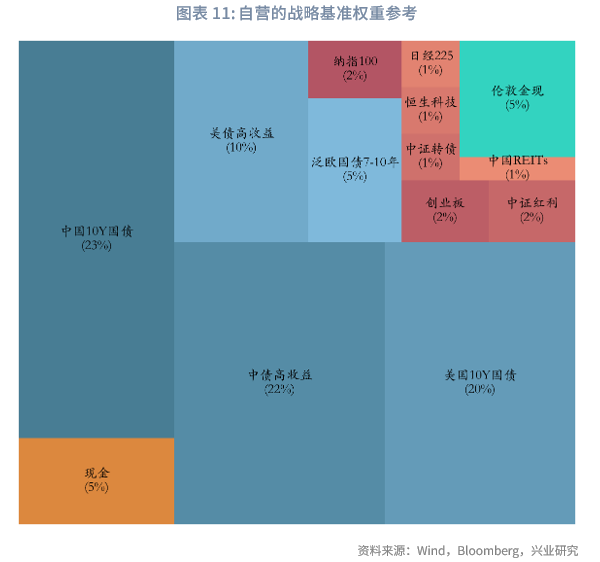
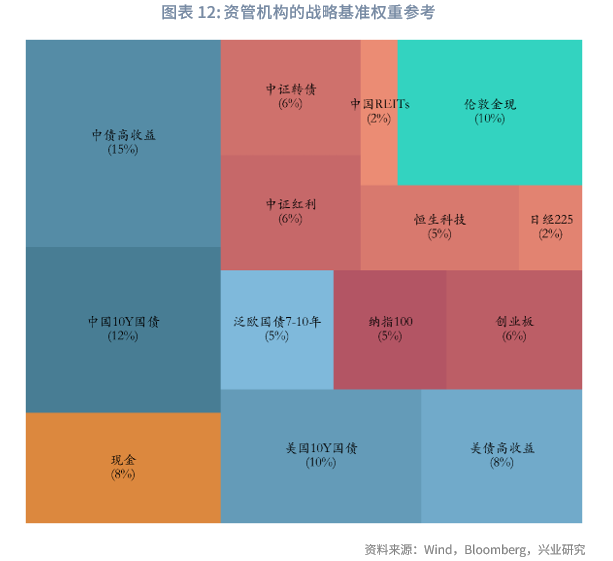
需注意的是，两类主体均以固收类资产作为配置底仓，具体结构与权重存在以下特征：对于资管机构，截至2025年9月底，股票型、混合型、债券型、货币市场基金占比分别为14.90%、9.22%、32.02%、40.28%，剩余为QDII、FOF基金等；若剔除货币基金，债券型基金在股票型、混合型、债券型基金中的占比达57%。而银行理财的固收资产比重更高。对于自营业务，固收类资产占比通常更大：上市券商自营的权益类资产占比平均约8%-15%，固收类占比则超过80%。商业银行自营中直接债券投资占比超80%，其余为基金、非标等；保险自营的债券投资占比约50%，股票、长期股权投资及基金占比约20%，剩余为银行存款等。上述背景下，本文设定两类主体的具体资产权重如下：自营的现金、固收、权益及类权益、商品权重占比分别为5%、80%、10%、5%；资管机构的对应权重则为8%、50%、32%、10%，各资产子类的具体权重可参见下图。

（2）基准模型与模型胜率参数设定

基准模型采用各类资产等权重配置。我们对比了“BL-战略基准版”的多个版本：无观点版（此处即战略基准配置）、生成主观观点版。其中，生成主观观点版的设置背景为：本研究仍以大类资产配置框架为核心，考虑到大类资产的主观观点获取难度较大，且即便可回溯，其样本期也相对较短，同时难以明确单个资产主观观点准确率达到何种水平时会产生显著超额收益。为此，我们设置了多个胜率水平：50%、60%、65%、70%、80%。

（3）BL模型主观观点生成方法

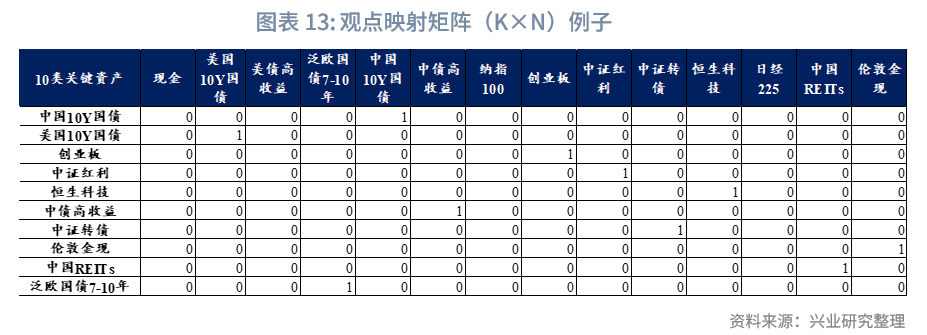
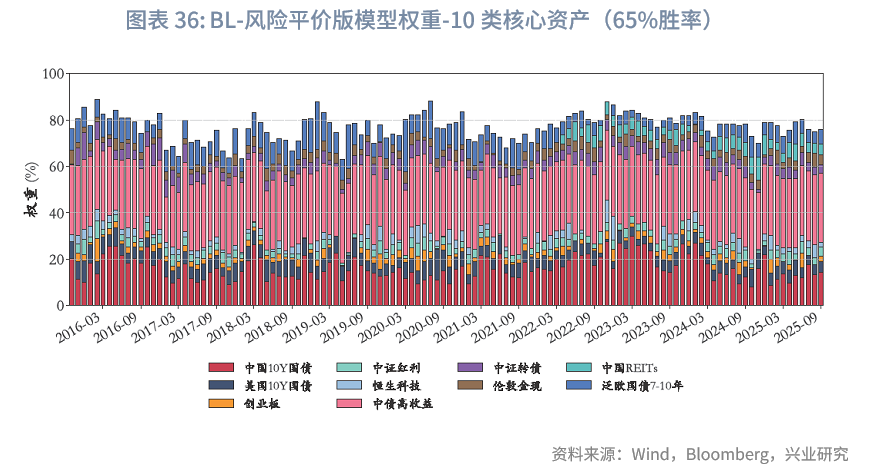
本研究基于历史收益率数据与预设胜率，生成具有可控正确率的模拟主观观点。结合当前覆盖的大类资产及研究特点，选取以下10类关键资产作为观点生成对象：中国10Y国债、美国10Y国债、创业板、中证红利、恒生科技、中债高收益、中证转债、伦敦金现、中国REITs、泛欧国债7-10年。具体构建方法如下：

观点映射矩阵P：从当前可投资资产中筛选关键资产，构建维度为K×N的观点映射矩阵P（K为关键资产数量，本文为10，N为全部可投资资产数量，本文为14）。矩阵中每一行对应一个观点的资产权重向量，仅在对应关键资产位置赋值1，其余位置为0，以此清晰标识观点所针对的具体资产。

观点不确定性矩阵Ω：基于历史月度收益率数据计算各关键资产的波动率，构建对角协方差矩阵Ω。矩阵对角元素为对应资产收益率的方差，直观反映观点所依赖历史信息的不确定性——资产历史波动率越高，对应观点的不确定性越大（即可信度越低）。

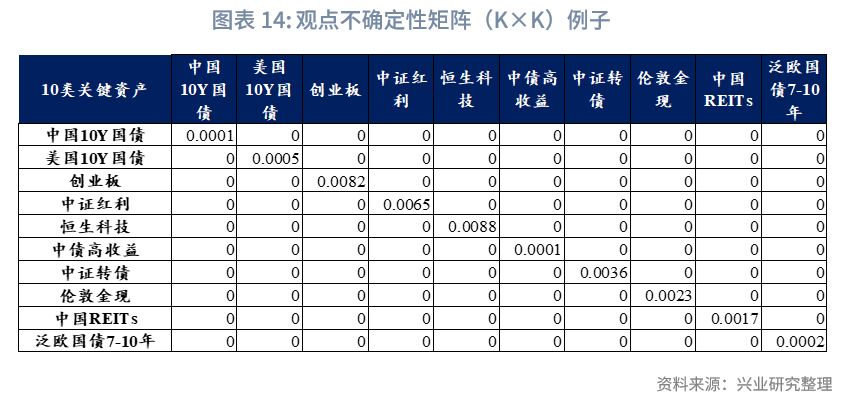
胜率参数与随机准确观点选择：为模拟现实中观点难以完全准确的特性，引入胜率参数（success rate）控制正确观点比例。通过随机抽样机制确定准确观点对应的资产（例如，10个关键资产在65%胜率下，经四舍五入后每月随机选取7个资产，使其观点准确反映未来收益方向；其余资产观点则设定为错误方向）。

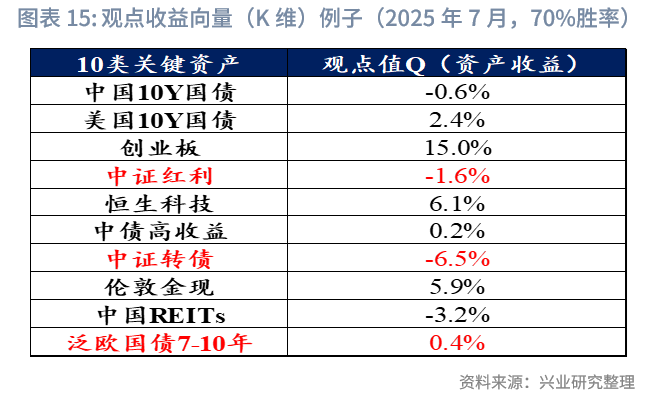
观点收益向量Q：从BL模型的推导逻辑来看，超额收益的核心定义为：资产预期下一期收益率相对无风险利率的超额部分。不过在实践场景中，超额收益的定义存在其他常见方式，例如直接定义为相对资产自身历史收益的超额部分，或简化为资产的实际收益预期。本文中，我们采用“资产收益预测”作为超额收益的定义标准，具体而言，是以主观观点收益向量所表征的、对资产下一个月（即下一期）收益率的预测值。观点值生成遵循以下规则：对于正确观点，其主观预测收益率为未来实际收益率的1.5倍，且预测超额收益率上限为15%（避免极端观点）；对于错误观点，采用对称惩罚方式，其主观预测收益率为未来实际收益率的-1.5倍，且预测超额收益率下限为-15%（避免极端观点）。该方法在控制观点正确率的同时，融合了历史波动率与未来收益信息的模拟逻辑，使BL模型在回测中更贴近实际投资决策的思维框架。以下是2025年7月（对8月预测）生成的观点收益向量，其中随机选取了7个资产作为正确观点（其余3个下表中标红的资产为错误观点，），其中创业板触发预测超额收益率上限15%。

（4）BL模型超参数与约束设置

参考行业通用设置，本文将风险厌恶系数λ设置为2，先验置信度缩放因子τ设置为0.25。

约束条件的设计充分考虑了实际投资场景中的合规要求与操作可行性，具体包括：

预算约束：要求全部资产权重之和为100%；

非负约束：不允许进行卖空操作；

集中度约束：单一资产权重上限为30%，以控制风险敞口；

平滑性约束：通过引入战略基准权重，约束新权重与旧权重之间的L1范数变化不超过40%，从而有效控制换手率与交易成本。

上述设置的核心逻辑在于：以战略基准权重为基础框架，通过融入主观观点对资产权重进行适度微调，实现既贴合基准又体现主动管理意图的配置目标。

（5）BL-战略基准版结果

在研究资产覆盖范围有限的场景下，BL策略需以更高胜率的主观观点作为边际安全垫，才能有效获取超额收益。具体而言，推荐当主观预测胜率达到60%~65%及以上水平时，在BL模型中嵌入部分核心资产的主观观点，可实现超额收益。

以资管机构的战略基准权重版本为例（自营版本可见附录，相关结果差异较小），根据2005年1月至2025年9月的回测结果，不同策略的表现对观点准确性存在显著依赖。数据显示，当BL模型中嵌入观点的胜率为50%时，其策略的总收益与年化收益均低于无任何主观观点的战略基准策略。值得注意的是，回测早期（如2005-2010年）核心资产数量较少（仅3个或5个），此时50%的胜率在实际计算中因四舍五入略高于50%（例如3类核心资产中选择2类准确，实际胜率为66.7%）；而后期扩展至10类关键资产时，50%胜率则恰好对应5类资产判断准确。尽管这类结果受随机因素影响，但仍可表明：在此胜率水平下，引入主观观点并未产生增量价值。

60%胜率较50%胜率已有提升，但2024年之前未表现出明显超额，其原因可从资产选择与组合权重特性两方面解释：在全部14类资产中，基于研究覆盖范围，我们仅对10类关键资产赋予主观观点；而在总权重之和为1的约束下，大类资产配置本质上体现为“相对权重”逻辑——即对某类资产的权重调整会间接影响其他资产的相对占比。这种情况下，即使10类关键资产的观点胜率达到60%（即6类判断准确），但受限于关键资产池规模及相对权重的联动效应，观点对组合收益的正向贡献仍难以有效释放，导致策略表现未能显著超越无观点的战略基准策略。

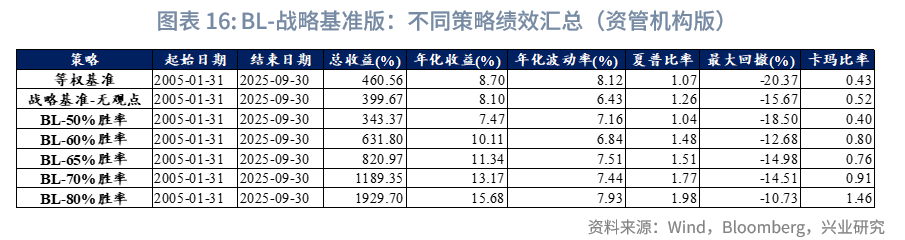
主观观点胜率60%~65%是BL策略相对等权基准及战略基准（无观点）版本有效获取超额收益的核心阈值：当胜率提升至65%时，BL策略（BL-65%胜率）表现显著跃升，年化收益达11.34%，夏普比率1.51，同时将最大回撤控制在-14.98%，卡玛比率0.76，各项核心指标均显著优于基准策略及低胜率BL策略。在此水平下，该模型相较等权基准、无观点的战略基准模型，不仅能长期获取约3%的年化超额收益，且组合波动率维持在更低或相当水平。从组合与组合内单个资产的横向对比来看，BL-65%胜率策略组合表现同样突出：年化收益可在所有单个资产中位列第3（仅次于纳斯达克指数与中证红利），夏普比率排名第4（仅次于现金、中债高收益债券以及中国10年国债）；波动率层面，其虽略高于固收类资产，但较权益类及类权益类资产显著更低。

若观点胜率进一步提升至80%，BL策略（BL-80%胜率）的收益与风险控制能力将再上台阶：年化收益15.68%（作为直观参考，本文基于“固收+”思路设定战略资产配置权重基准，样本期内中债-高收益债券、中债10年期国债的年化收益率分别仅为6.3%和4.5%），夏普比率达1.98，最大回撤更是收窄至10.73%；同时，其回撤后修复能力突出，卡玛比率大于1，展现出极强的风险调整后收益优势。

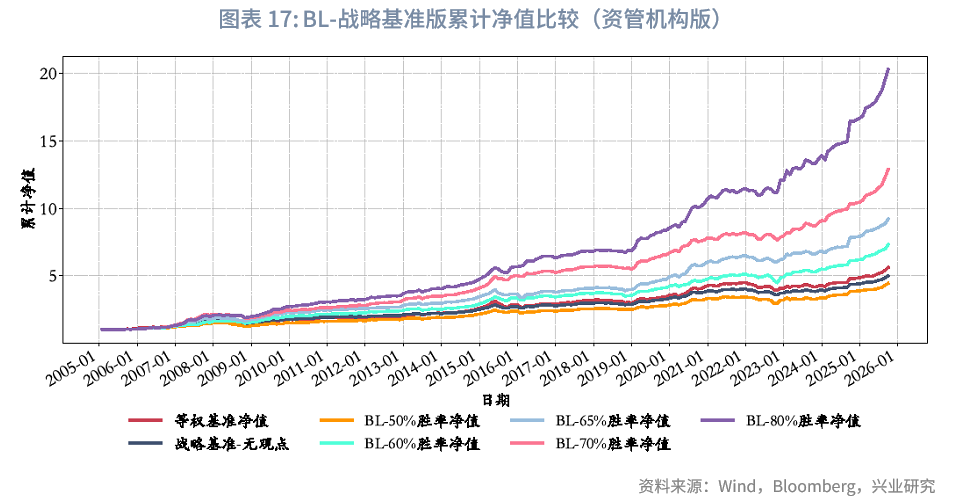
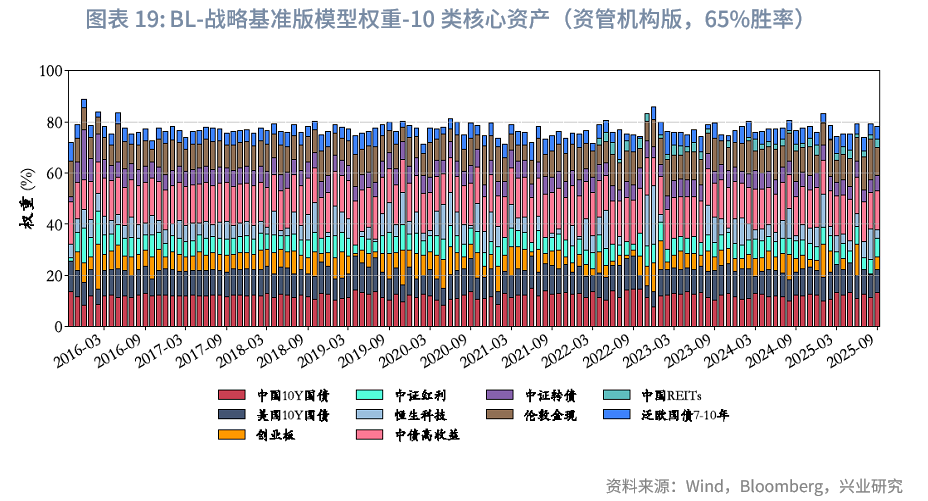
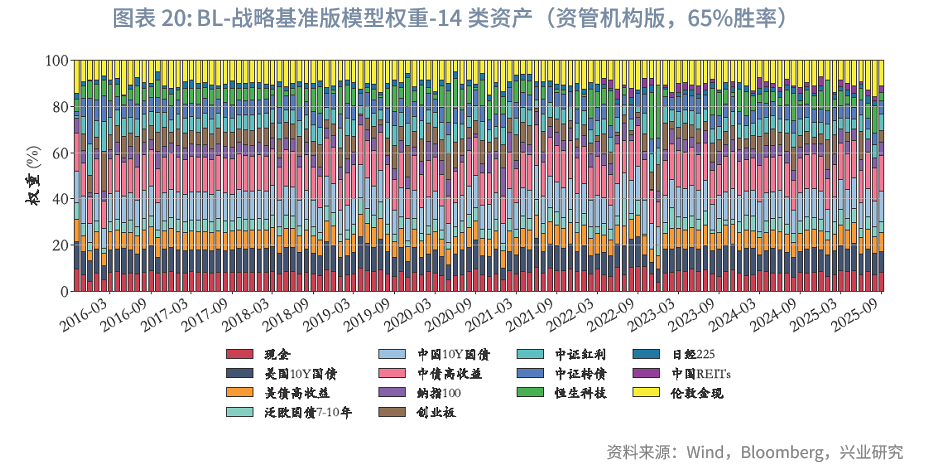
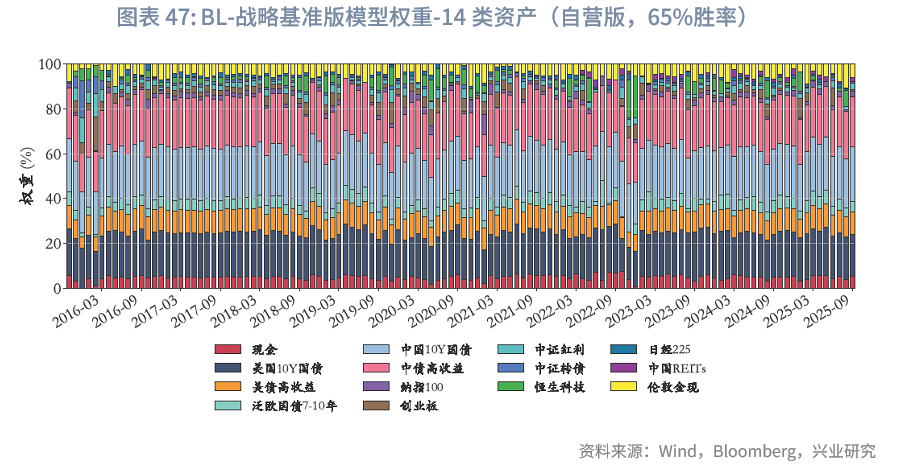
战略基准下的权重微调：在资管机构版本的基准权重中，10类核心资产的权重占比为84.6%。从这10类核心资产的月度权重调整情况来看，由于设置了预算约束、非负约束、集中度约束及平滑性约束，其调整幅度符合“在战略基准上微调”的实务操作需求。样本期内，考虑到中国REITs上市时间较晚，2022年4月之后，这10类核心资产的平均权重合计约77.4%。仅在主观观点判断10类核心资产中绝大部分表现不佳时，才会对其进行较大幅度减配。以2020年5月为例：该月10类核心资产中，中国10Y国债、中证转债、中证红利、创业板资产收益率为负，美国10年国债、泛欧国债7-10年收益基接近0，核心资产整体表现偏弱，而恒生科技当月表现强劲，涨超5%。在此市场环境下，基于65%胜率生成的主观观点缩减中证转债等资产配置比例，将恒生科技配置比例提高了4.2%。

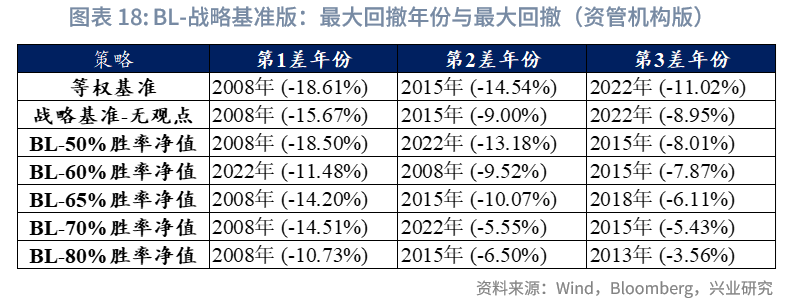
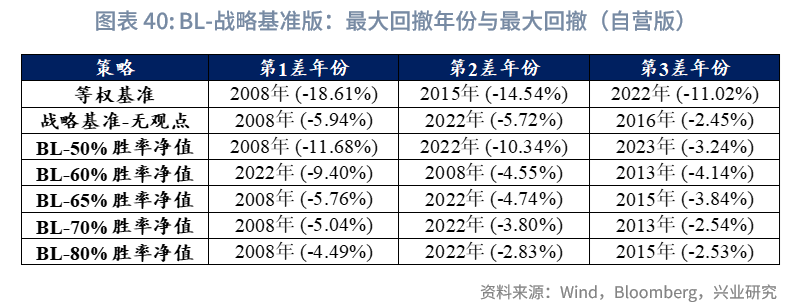
最大回撤年份分析：大类资产配置的最大回撤通常出现在系统性风险集中爆发的年份（如2008年），这与“资产池选择与样本期”部分中各类资产年度收益率、波动率的统计结论相吻合。2008年期间，组合内仅现金、泛欧国债7-10年、伦敦金、中债高收益、美国10Y国债、中国10Y国债这6类资产实现正收益，其余资产跌幅普遍接近40%。在此背景下，BL-65%胜率组合的回撤仅为14.20%，除上述6类正收益资产外，该回撤表现优于其他所有单一资产。从权重调整来看，2008年3月金融危机启动后，中证红利、纳指100的当月权重分别从13.4%、10.9%下调至接近0；与之对应，伦敦金权重从7.7%上调至接近20%，通过仓位调整对冲风险。类似地，2020年全球流动性宽松后，2022年全球进入加息紧缩周期，此时组合内仅现金、伦敦金、中国10Y国债、中债高收益、中国REITs这5类资产实现正收益。权重调整上，恒生科技、纳指100的权重较前期高点分别下降约12%和3%，中国10Y国债、中债高收益的权重则分别增配约1~3%，通过仓位微调，除了上述正收益资产之外，BL-65%胜率策略组合2022年回撤仅比中证红利略大，优于其余8个资产。

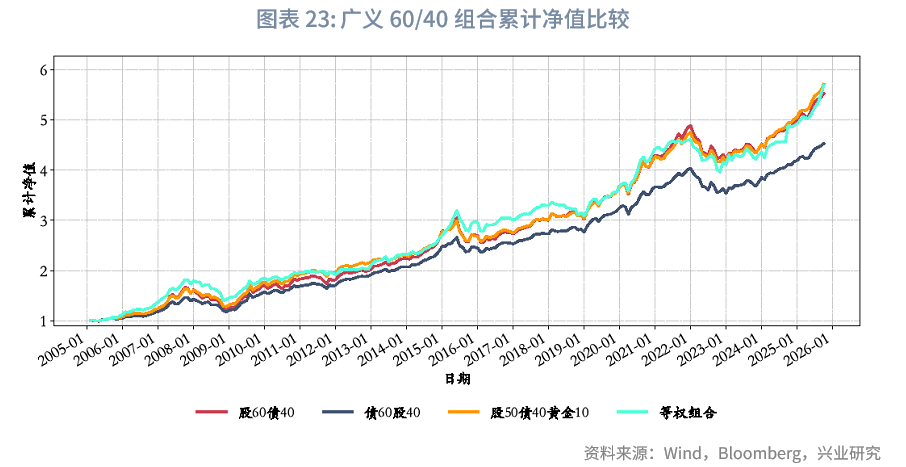
3.1.4 广义60/40组合

为了考虑流动性，我们设计了三个版本的广义60/40组合模型：（1）股60债40：固定现金仓位5%，95%可配置资产中股票占比60%、债券占比40%；（2）债60股40：固定现金仓位5%，95%可配置资产中债券占比60%、股票占比40%；（3）股50债40黄金10：固定现金仓位5%，95%可配置资产中股票占比50%、债券占比40%、黄金占比10%。

组合权重方面，广义60/40组合均采用固定权重配置方案，每月仅需先明确可配置资产池（例如判断部分指数当月是否有可用数据），具体细节此处不再赘述。

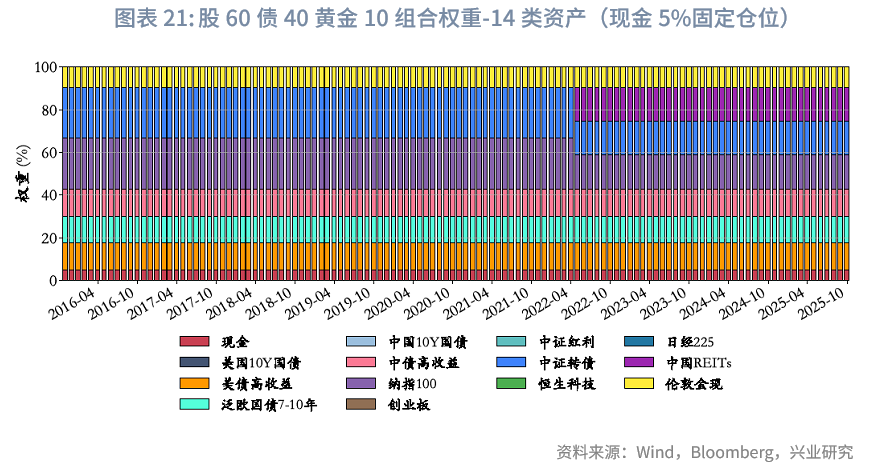
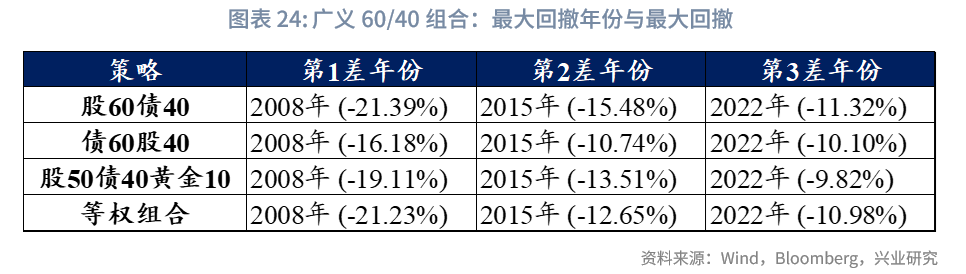
风险收益方面，样本期内，股50债40黄金10略优于股60债40策略，债60股40风险收益比较高。股50债40黄金10优于股60债40策略，核心是收益与风险平衡更优：其年化收益（8.80%）略高于股60债40（8.63%），风险却更低，年化波动率（8.16%）、最大回撤（-21.92%）均小于股60债40（9.18%、-26.66%），且夏普比率（1.08）更高（股60债40为0.94），“风险-收益”性价比更优。债60股40策略则以稳健为主要特征，虽年化收益（7.59%）在四类策略中最低，但风险控制表现突出，年化波动率和最大回撤均处于低位，风险调整后收益（夏普比率1.10）亮眼，是典型的低风险、稳健型配置选择。

3.1.5 永久投资组合

本文参考Harry Browne原版永久投资组合，采用等权配置（各25%）四大类资产：权益及类权益、固定收益、现金、黄金，且各大类下的资产小类亦按等权分配。

组合权重方面，因该组合已包含25%权重的现金，故无需额外考虑流动性，其余细节此处不再赘述。

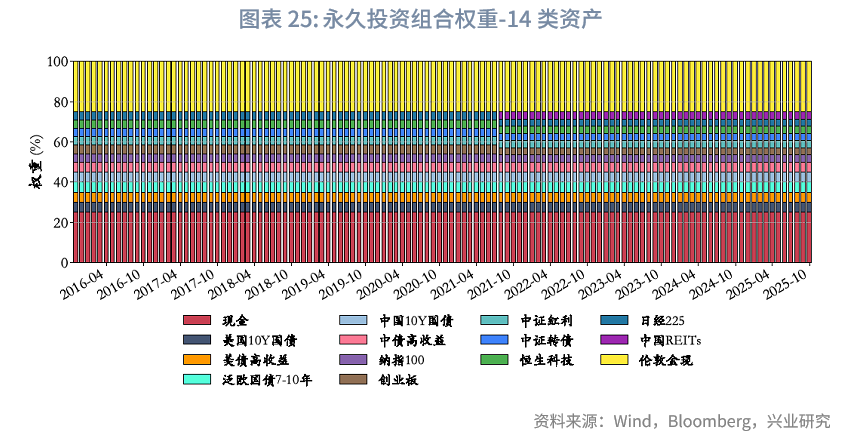
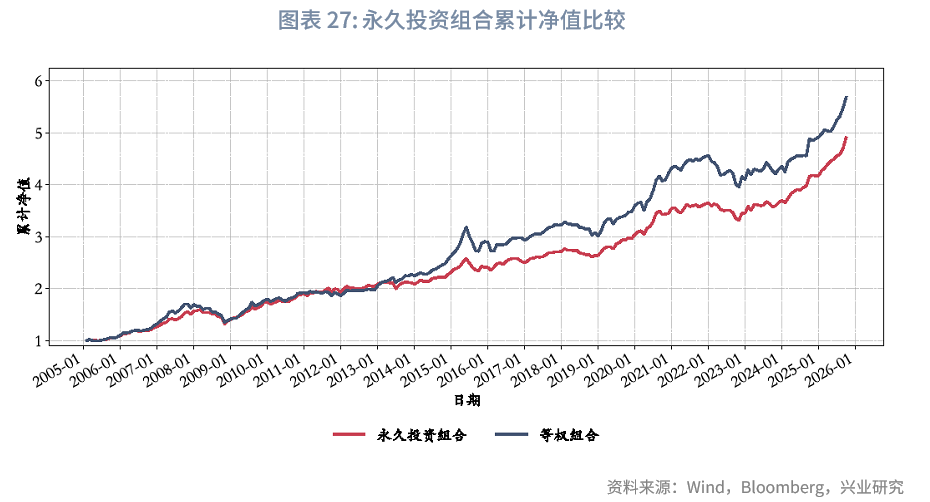
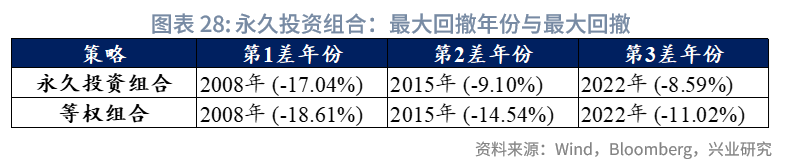
风险收益方面，样本期内，永久投资组合策略几乎严格优于等权策略。二者收益接近，永久投资组合年化收益8.00%，等权组合年化收益8.77%；但永久投资组合波动显著更小，年化波动率6.65%，等权组合为8.12%；回撤更低，最大回撤-17.04%，等权组合为-20.41%；且夏普比率更高，达1.20，等权组合为1.08。从最大回撤年份来看，得益于25%现金的配置缓冲，2008年永久投资组合回撤17.04%，低于等权组合的18.61%。总结来看，永久投资组合通过提高现金比重，有效减少了组合波动与回撤，且收益未出现明显下降。

3.1.6 风险平价模型

本文主要采用的是实务简化版本，即波动率倒数版本；协方差版本风险平价模型的结果，可参见附录“风险平价模型-协方差版相关结果”，该版本结果回撤较大且稳定性欠佳。

我们设计的风险平价策略分为三个版本：（1）纯粹风险等权（基准版本），95%权重按非现金资产历史波动率倒数分配（确保各资产风险贡献相等），剩余5%固定为现金权重；（2）“风险平价-带权重限制”，在纯粹风险等权版本基础上增设单资产30%权重上限：若资产权重超出上限则固定为30%，剩余权重重新分配以维持风险平价；（3）“风险平价-结合主观观点”，以纯粹风险等权版本为基础，对核心资产按不同胜率施加主观观点调整，并通过相对超额幅度差异化处理波动率（进而影响权重）：先通过“资产未来实际收益/历史最大绝对收益”计算相对超额幅度，量化资产收益偏离自身历史水平的程度；再根据主观观点判断准确性（正确/错误）与资产未来收益方向（正/负），差异化生成基础调整因子，若观点正确且资产未来上涨，基础因子按“0.7-相对超额幅度×0.2”计算（相对超额幅度越高，因子越低，波动率降幅越大），若观点正确且资产未来下跌，基础因子则按“1.5+相对超额幅度×0.5”计算（亏损幅度越大，因子越高，波动率增幅越大）；同时叠加±0.05或±0.1的随机扰动，避免单一观点的极端影响。最终，通过调整后的波动率间接优化风险平价权重，让“高超额收益且判断正确”的资产获得更高配置，“亏损且判断正确”的资产降低权重。此外，我们设置了50%、60%、65%、70%、80%多个胜率水平。

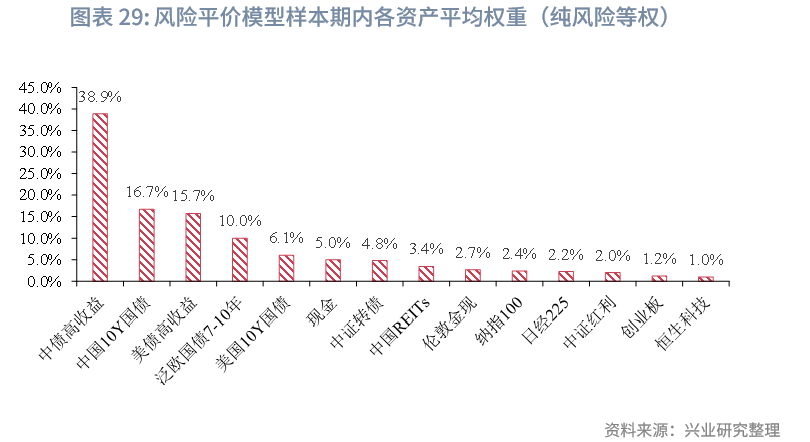
组合权重方面，因现金波动率极低，若纳入风险平价计算易导致权重过高，且其核心作用是应对流动性冲击而非参与风险收益配置，故不纳入风险平价范畴，本文中现金资产固定分配5%权重，剩余95%权重通过风险平价机制分配给非现金资产。在样本期内各资产平均权重分配上：（1）“纯粹风险等权”，中债高收益因其整体波动较小（详见“资产池选择与样本期”部分），平均权重可达39.0%，后续中国10Y国债、美债高收益、泛欧国债7-10年、美国10Y国债的平均权重分别为16.7%、15.7%、10.0%、6.1%，从整体看，固收资产权重总和达87.4%，因此在纯粹风险等权规则下，风险平价模型是名副其实的固收+组合；（2）“风险平价-带权重限制”，在引入单个资产30%权重上限后，中债高收益平均权重降至28.8%，中国10Y国债、美债高收益、泛欧国债7-10年、美国10Y国债的平均权重分别为19.9%、16.3%、11.5%、7.1%，整体固收资产权重总和为83.6%；（3）“风险平价-结合主观观点”，以65%胜率版本为例，中债高收益、中国10Y国债、美债高收益、泛欧国债7-10年、美国10Y国债的平均权重分别为37.9%、16.4%、15.1%、10.9%、6.1%，整体固收资产权重总和为86.4%。

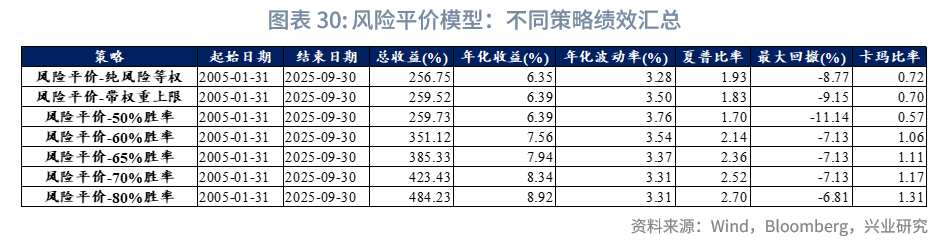
风险收益方面，样本期内，因组合权重整体偏向固收类资产，风险平价模型整体呈现较高夏普比率。其中，纯风险等权策略年化收益为6.35%，年化波动率控制在3.28%的较低水平，夏普比率达1.93；与组合内单个资产相比，该策略年化收益与美债高收益相当（详见附录“大类资产年化收益率和波动率”），且波动率低2个百分点，夏普比率高0.7。进一步来看，通过引入主观观点对策略进行优化后，其收益能力显著提升，当主观观点胜率达到60%时，策略表现实现关键性跃升：在保持与纯风险等权基准相近的年化波动率（3.37%）的同时，将年化收益大幅提升至7.94%。这一优化使策略夏普比率达到2.36，明显高于纯风险等权策略的1.93。

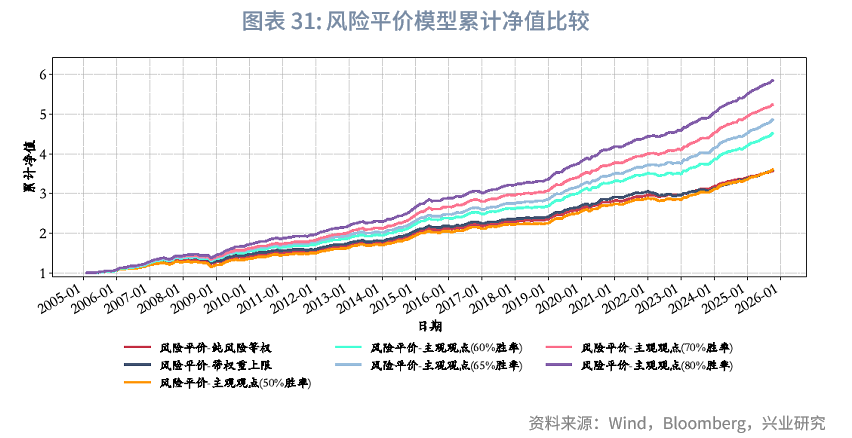
由于后文“Black-Litterman-风险平价模型”部分将以风险平价模型（无观点）版作为基准，此处暂不对模型权重调整展开过多描述（权重变动详情可见附录“风险平价模型结果”）；而在最大回撤控制上，风险平价模型族表现更为突出。

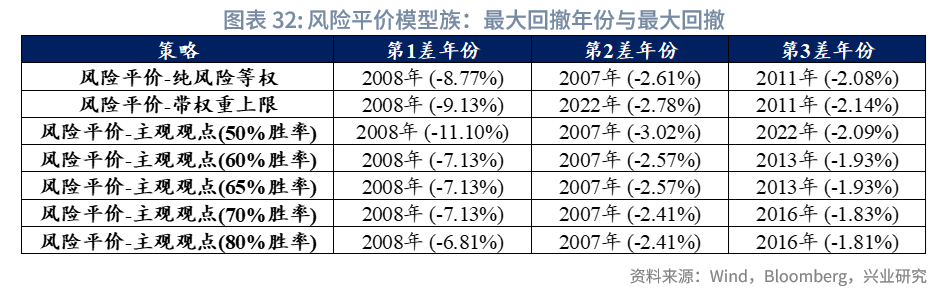
3.1.7 Black-Litterman-风险平价模型

（1）基准权重（Wmkt）设置

“BL-风险平价”与“BL-战略基准”的核心差异在于市场组合初始权重向量的构建逻辑：“BL-战略基准”以集团或理财子公司的战略基准为权重设定基础，“BL-风险平价”则基于风险平价模型计算初始权重，通过让各类资产贡献相对均衡的风险奠定配置基础。

其风险平价初始权重计算规则为：现金资产固定分配5%权重——因现金波动率极低，若参与风险平价易导致权重过高，且其核心作用是应对流动性冲击而非风险收益配置，故不纳入风险平价计算；剩余95%权重分配给非现金资产，以上月末为基准，基于上一完整月度的日度收益率数据计算各非现金资产波动率，按“权重与波动率成反比”原则（即单个资产波动率倒数占所有非现金资产波动率倒数总和的比例）确定权重。

（2）基准模型与模型比较

我们对“BL-风险平价”的多个版本展开对比，具体包括基准（各类资产等权重）、无观点版（风险平价权重）与生成主观观点版；其中主观观点的胜率水平仍设置为50%、60%、65%、70%，且观点生成方法与“BL-战略基准”完全一致，此处不再赘述。

（3）BL-风险平价模型结果

在主观观点加入时机上，与“BL-战略基准”得出的结论保持一致：推荐当主观预测胜率达到60%~65%及以上时，在BL模型中嵌入部分核心资产的主观观点，能够有效实现超额收益。

“BL-风险平价”与“BL-战略基准”的核心差异聚焦于风险与收益特征的侧重不同：前者更注重波动率与回撤的精细化控制，因而能实现更高的夏普比率，但长期年化收益会低于后者。例如，风险平价（无观点）[1]模型在样本期内可实现1.93的夏普比率，该数值略高于BL-战略基准-资管-65%胜率模型；同时，其年化波动率仅为3.23%，低于之前的所有模型，最大回撤8.77%也小于等权基准及BL-战略基准-资管（无观点）模型，而其6.24%的年化收益，则低于等权基准（8.70%）与BL-战略基准-资管（无观点）（8.10%）。进一步从两者对比可见，面对不同基础模型时，BL模型能有效融入主观观点，其更核心的价值在于作为“主观观点嵌入框架”的灵活性——能够与风险平价、战略基准等不同基础模型或各类配置需求相结合，而非局限于单一的风险或收益目标。

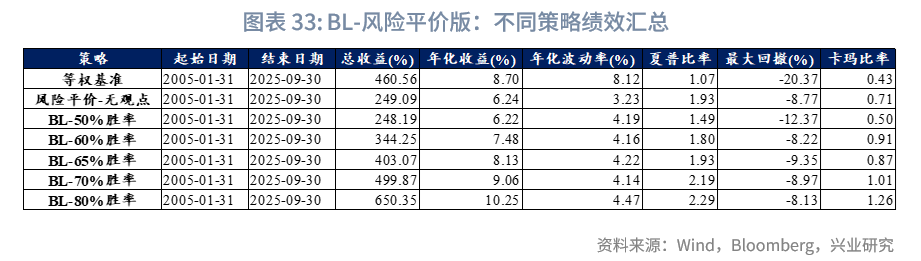
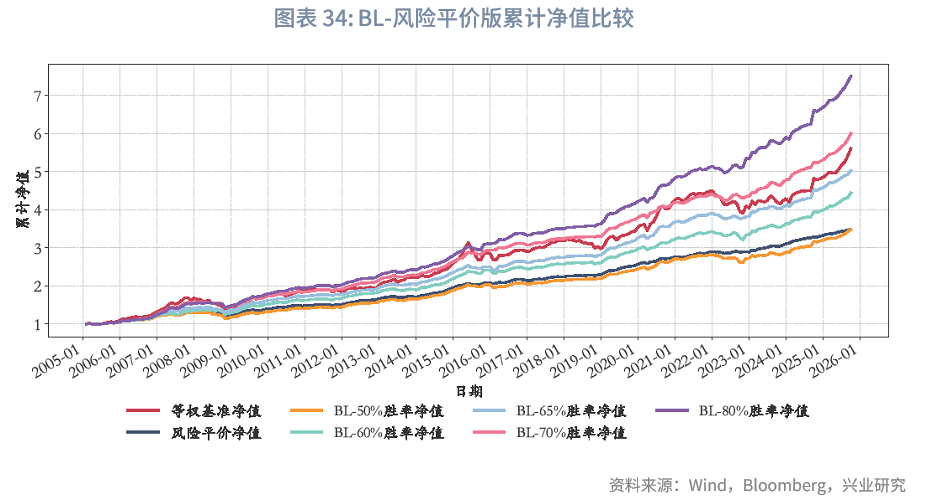
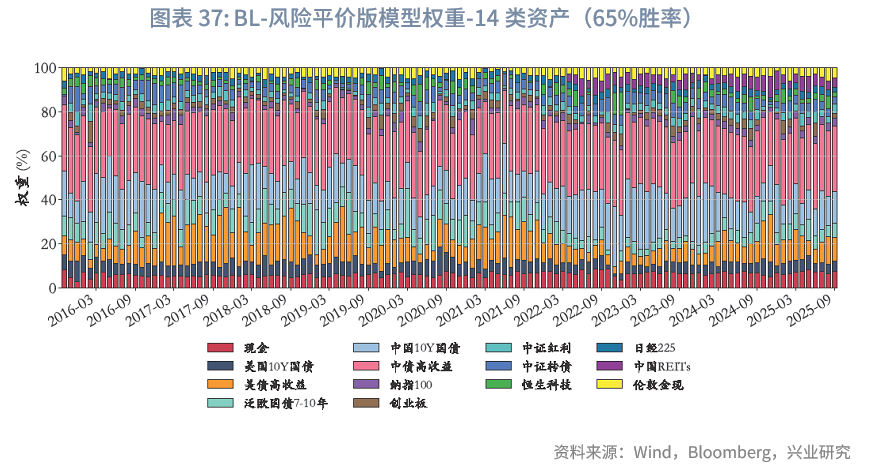
风险平价下的权重微调：与“BL-战略基准”模型不同，“BL-风险平价”模型未预设初始权重，而是由风险平价提供，且与“风险平价模型”中“纯风险等权”版本一致。在“BL-65%胜率-风险平价”下，在核心10类资产中，其整体平均权重之和约为84.6%，其中平均权重较高的几类资产依次为中债高收益、泛欧国债7-10年、中国10Y国债、美国10Y国债。固收类资产中，中债高收益、中国10Y国债、美债高收益、泛欧国债7-10年、美国10Y国债的平均权重分别为28.8%、17.2%、14.8%、10.3%、6.5%，整体固收资产权重总和为78%，与“风险平价-65%胜率”版本的86.4%存在差异，可能原因如下：（1）BL模型纳入主观观点采用贝叶斯思路，通过调整初始市场隐含均衡收益影响最优化求解，而风险平价模型则通过直接建立主观观点超额收益与波动率预期的映射进行调整，未纳入对观点不确定性的考量；（2）BL模型包含投资者风险厌恶系数、市场均衡信念等超参数，也会导致差异。两种模型纳入主观观点的方式难分绝对优劣，通常而言，风险平价的方式更主观直白，从主观观点到超额收益、波动率再到权重基本呈线性映射；而BL模型的兼容性则更强。

最大回撤年份分析：以65%胜率为例，与“BL-战略基准版”相比，“BL-风险平价版”的初始权重由风险平价机制计算得出，2008年日经225、纳指100、中证红利的权重基本在年底降至0，而2008年1月时，上述资产的权重总和为16.8%。相较于“BL-战略基准版”事先设定基准权重的模式，风险平价模型对资产波动的敏感性更高，因此在极端回撤场景下，其回撤控制能力也更为出色，尤其适合对风险与回撤要求极高的机构。此外，“BL-风险平价版”在其余年份的最大回撤，基本都控制在3%以内。

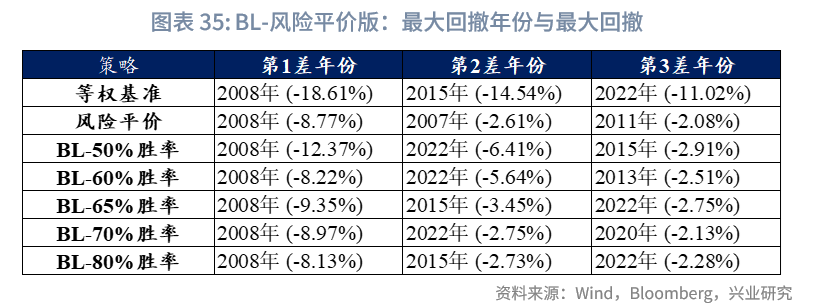
3.1.8 模型总结

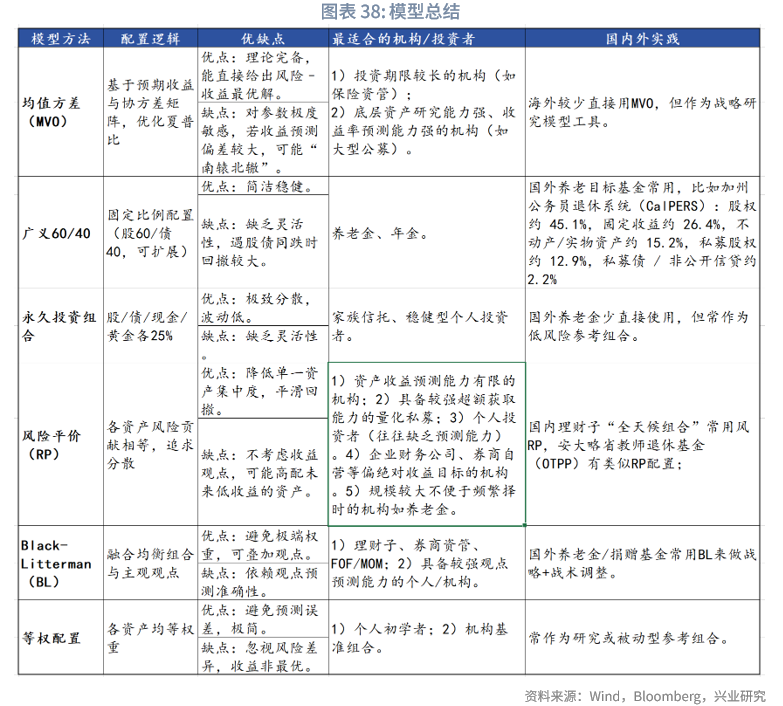
在多资产投资实践中，均值–方差优化（MVO）、广义60/40组合、永久投资组合、风险平价（RP）、Black-Litterman（BL）以及等权配置等方法，是最具代表性的几类配置框架。不同模型在理论基础、参数依赖、适用机构和实际效果上均存在差异，需要结合资金性质、研究能力与风险偏好进行取舍。

首先，均值–方差优化（MVO）以夏普比率最大化为目标，能够在理论上给出风险收益最优解。该模型的优点在于逻辑完备，能够直接利用收益率和协方差矩阵的信息进行优化，并可通过调整预期收益率等方式叠加投资者的主观预测。但其缺点也十分突出：对预期收益和协方差的估计极为敏感，一旦预测偏差较大，容易导致“南辕北辙”的结果，甚至出现权重集中于少数资产的情况。因此，MVO更适合投资期限较长、具备较强底层资产研究和收益率预测能力的机构，如大型公募基金。在国际实践中，海外较少直接用MVO，但作为战略研究模型工具。

与之相比，广义60/40组合更为简洁稳健。其典型形式是股票和债券的固定比例配置，并可扩展至类权益（如可转债、REITs）、商品等多类资产。该方法的优势在于透明、易执行，且在长期历史中表现稳健，能够作为许多养老金和年金资金的核心框架。但其劣势也较为明显：缺乏灵活性，在股债同跌的极端市场中往往面临较大回撤。国外养老目标基金常用广义60/40组合，比如加州公务员退休系统（CalPERS）：股权约 45.1%，固定收益约 26.4%，不动产/实物资产约 15.2%，私募股权约 12.9%，私募债/非公开信贷约 2.2%。

进一步分散的永久投资组合，通过股票（权益和类权益）、债券、现金和黄金的等比例配置，力求覆盖不同经济环境，实现极致分散和低波动。该方法的优点是对经济周期具有较强的适应性，回撤控制较好，但缺点在于在权益牛市阶段明显跑输股市，长期超额有限。因此，该组合更适合养老金、家族信托以及追求财富保值的保守型个人投资者。国外养老金较少将其作为核心框架，更多用作低风险参考组合。

近年来受到广泛关注的风险平价，通过让各类资产在组合中贡献相等风险，实现风险来源的均衡化。其优点在于能够显著降低单一资产对组合的冲击，提高夏普比率，并在历史上展现出稳健的回撤控制能力。然而，该方法存在两方面局限：一是依赖杠杆提升收益，对衍生品与利率工具的使用要求较高；二是未显式纳入收益率预期，如果某一时期某类资产的预期收益偏低，风险平价仍可能给予其较高权重，从而导致潜在的机会成本。基于这些特点，风险平价更适合：1）追求稳健的养老金、银行理财子公司；2）具备较强单一资产超额获取能力的量化私募；3）缺乏预测能力的个人投资者；4）资金体量庞大、不支持高频择时的机构（如社保基金、养老金）。在国际实践中，美国俄亥俄州公务员退休系统（OPERS）和德州教师退休系统（TRS）均设有风险平价组合，富达投资（Fidelity）还专门推出了Risk Parity Fund。在中国，风险平价理念已逐步被理财子公司采纳，并常见于“全天候组合”的设计中。

Black-Litterman（BL）模型则在MVO的基础上引入市场均衡组合，并可叠加投资者的主观观点。其优点是能有效缓解MVO权重极端化的问题，避免组合集中于少数资产，同时允许投资者根据研究结论灵活调整权重。但BL模型的挑战在于依赖观点预测的准确性，同时参数设定较复杂。该方法适合理财子公司、资管机构、FOF/MOM管理人等需要在均衡配置基础上叠加行业或主题观点的机构，也适合具备较强资产预测能力的个人投资者。在国际上，BL模型广泛应用于养老金与捐赠基金的战略与战术配置中；在中国，公募FOF和部分理财子公司已披露采用BL框架。

最后，等权配置以各资产等权分配为原则，优势在于极简透明，能够有效避免预测误差，是个人投资者或机构进行基准对照的常用方法。但其缺陷在于完全忽视资产的风险差异，导致组合的风险收益表现并非最优。因此，该方法主要适合初学者或作为参考组合使用。

综上所述，不同配置模型在实践中各具适用性。MVO和BL适合研究能力较强、能够形成明确主观观点的机构；风险平价和广义60/40更契合养老金、年金等长期稳健型资金；永久投资组合与等权配置则为保守型或个人投资者提供了简便易行的长期框架。在国际实践中，大型养老金通常结合MVO、BL与风险平价的方法，在战略配置和战术调整中灵活运用；在中国，养老金和理财子公司则更多采用广义60/40与风险平价的混合式方案，并在部分领域引入BL，以适配本土市场环境与监管要求。

四、低波组合的构建方法

4.1.1 路径1：提高固收类资产比重

本文“三、大类资产配置方法实践与比较”部分已对主流大类资产配置模型展开比较，结论显示：仅从低波表现来看，固收类资产在组合中的占比是影响低波效果的关键因素。

对上述资产配置模型分别按单年度最大回撤率与年化波动率排序（涉及胜率的模型统一设定65%胜率，广义60/40组合选取“股票50%、债券40%、黄金10%”的配置结构）：单年度最大回撤方面，排序为风险平价-65%胜率（7.13%）＜BL-战略基准-自营-65%胜率（9.02%）＜BL-风险平价-65%胜率（9.35%）＜永久组合（17.04%）＜BL-战略基准-资管机构-65%胜率（14.20%）＜等权组合（18.61%）＜广义60/40（19.11%）＜均值方差（40.00%）；年化波动率方面，排序为风险平价-65%胜率（3.37%）＜BL-风险平价-65%胜率（4.22%）＜BL-战略基准-自营-65%胜率（4.77%）＜永久组合（6.65%）＜BL-战略基准-资管机构-65%胜率（7.51%）＜等权组合（8.12%）＜广义60/40（8.16%）＜均值方差（16.29%）。

从波动表现最优的前两类组合来看：“风险平价-65%胜率”固收占比86.4%，现金占比5%；“BL-战略基准-自营-65%胜率”的固收类资产占比80%、现金占比5%；“BL-风险平价-65%胜率”与组合的固收类资产占比处于75%-78%区间（接近80%），现金占比同样为5%。其余组合的资产结构中固收类资产占比如下：“永久组合”的固收类资产与现金权重各为25%；“BL-战略基准-资管机构-65%胜率”的固收资产占比50%、现金占比8%；“广义60/40组合”（股票50%、债券40%、黄金10%）的固收类资产占比40%；“等权组合”的固收类资产合计占比约35.7%，同时配置5%现金。可见，上述组合的单年度最大回撤与年化波动率，基本与固收类资产占比呈负向关系，从附录“大类资产年化收益率和波动率”的数据中得到印证，其中现金年化波动率仅0.16%，中美高收益债及中国10年期国债的年化波动率亦控制在5.5%以内。

需特别指出的是，风险平价模型可作为低波组合的标杆：其核心理念是各类资产风险贡献等权，由此构建的组合本身已具备较强的波动控制能力。若组合中固收类资产的平均占比高于风险平价模型的建议水平，则意味着人为进一步压缩了权益等风险资产的风险预算。综上分析，若要进一步降低组合波动，最直接的方式是将固收类资产占比提升至90%-95%区间，即提高固收资产的风险预算。

4.1.2 路径2：组合中加入低相关资产

本文所选取的常规14类资产，已基本覆盖主流大类资产配置品种。若需进一步在大类资产配置中加入低相关资产以降低波动，主要可考虑以下两类：一类是私募策略（如CTA策略、宏观对冲中性策略、指数增强策略等），这类策略之所以能实现低相关性，核心在于多数采用套利逻辑，因此与商品等基础资产的相关性较低；另一类是新兴资产，例如稳定币，当前属性上较符合低波动、低相关的特征，待未来法律监管框架逐步成熟后，也可成为一类可选资产。

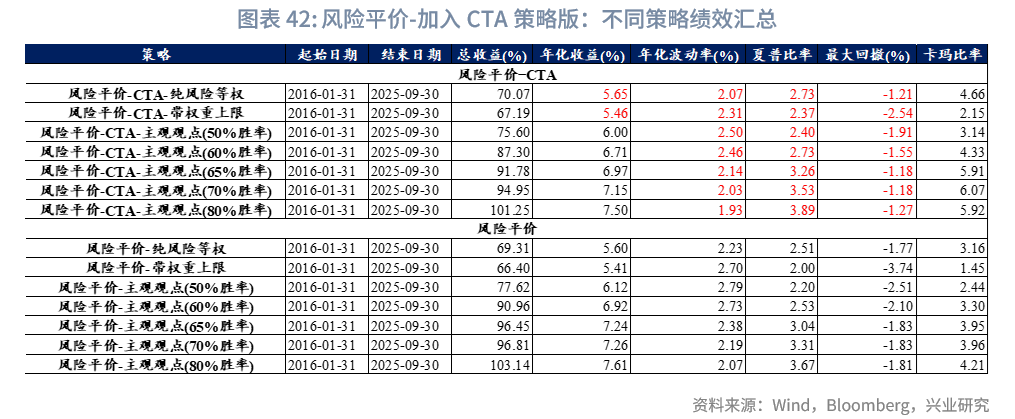
本文尝试在14类资产基础上加入CTA策略资产，通过对比加入前后的风险收益变化，检验CTA资产能否有效降低组合波动。测试基准模型选用风险平价模型，由于CTA策略指数的起始时间限制，回测对比的时间范围设定为2016年至2025年9月底。从CTA策略自身表现来看，其年化收益率、年化波动率、夏普比率、最大回撤分别为10.75%、6.03%、1.78、3.87%，其中夏普比率在本文所有大类资产中排名第三，最大回撤为除现金外最低，年化波动率则略高于固收类资产。

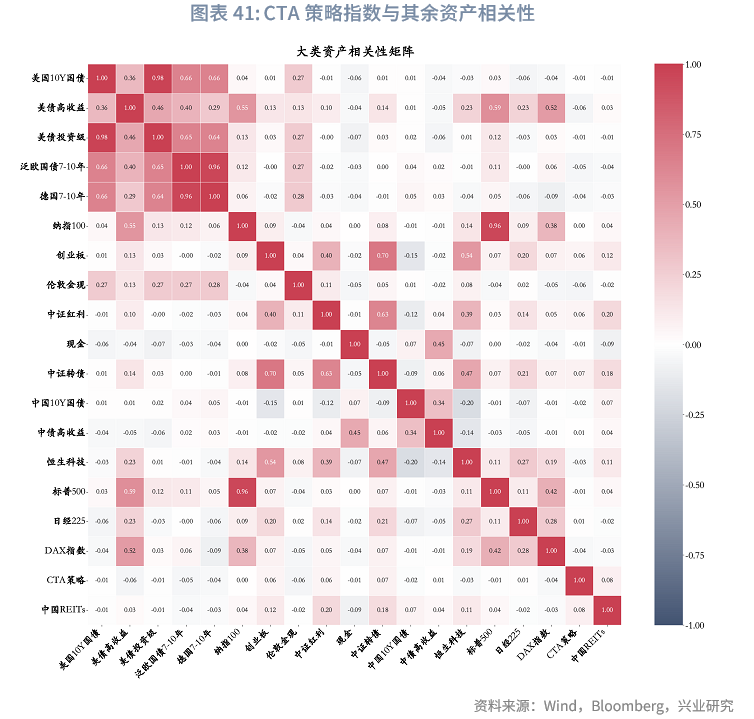
从相关性分析结果来看，CTA策略指数与多数资产呈负相关或低相关关系，其中与该指数相关性最高的资产为中国REITs，相关系数也仅为0.08。从组合表现来看，加入CTA策略后，组合波动显著降低，同时获得更高的夏普比率。与未加入CTA策略的基准组相比，在所有胜率场景下，加入CTA的风险平价模型波动率、最大回撤均有所下降，且夏普比率明显提升，这表明加入CTA策略在未显著牺牲收益的前提下，有效降低了组合波动。

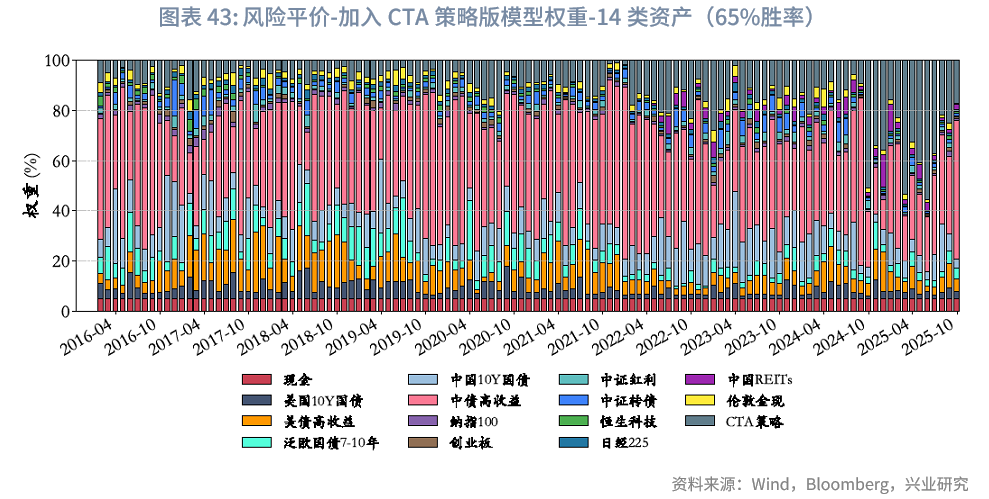
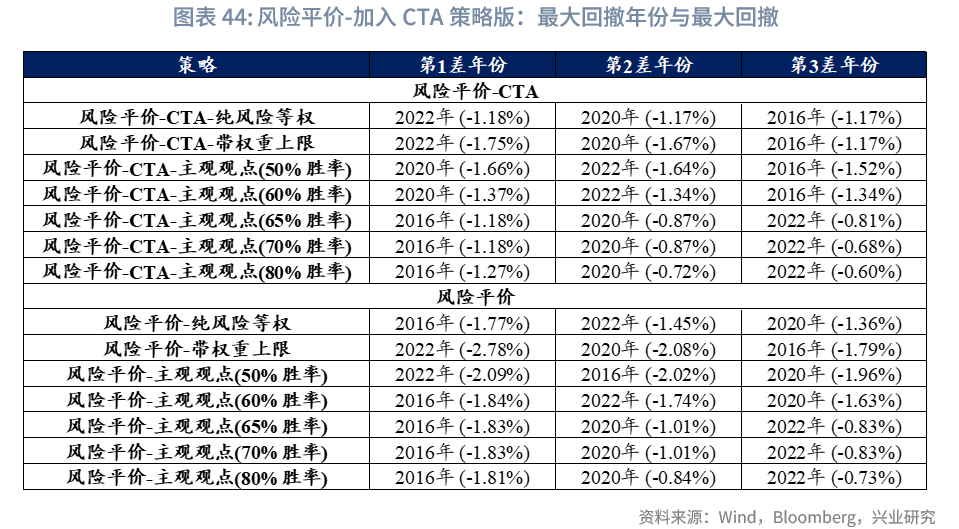
单年度最大回撤方面，由于样本期未覆盖2008年（通常是大类资产配置最大回撤年份）、2011年、2013年等其他大类资产配置表现较差的年份，故仅选取2020年、2022年（通常为其他大类资产配置表现第二、第三差的年份）进行对比。结果显示，相较于纯风险平价模型，加入CTA策略后，这两个年份的最大回撤减少超1%；若与其他模型相比，回撤降幅则更为显著。从风险平价模型给出的资产权重来看，CTA策略在整个回测期间的平均权重为13%，2022年之后其平均权重进一步提升至19.5%。

五、参考文献

1.林雷, 刘黎明, 张诚, 2025. 我国城镇职工基本养老保险可持续性研究——基于养老金入市和国有资本划转政策的测算[J]. 财政科学(04): 92-107.

2.孟勇, 任梦, 赵心, 2022. 行业资产的Black-Litterman模型配置研究——基于社交网络情绪文本挖掘算法[J]. 数量经济技术经济研究, 39(01): 154-173.

3.庞杰, 2021. Black-litterman模型下行业资产配置——结合投资者情绪指数[J]. 科研管理, 42(06): 17-24.

4.宋正阳, 周忠宝, 余乐安, 等. 基于混合集成预测算法和Black-Litterman模型的投资组合优化策略研究[J]. 中国管理科学: 1-12.

5.王莹, 潘文捷, 2022. 基于投资时钟和Black-Litterman模型的全球股市行业动态配置研究[J]. 数量经济研究, 13(03): 36-53.

6.王玉国, 2018. 基于风险平价策略的高净值客户资产配置研究[J]. 北京社会科学(06): 119-128.

7.乌云高, 2022. 基于Black–Litterman的养老金最优资产配置模型研究[D]. 华北电力大学.

8.姚海祥, 李晓鑫, 房勇, 2023. 基于AdaBoost集成算法和Black-Litterman模型的资产配置[J]. 系统工程理论与实践, 43(11): 3182-3196.

9.周静, 2024. 基于Smart Beta策略的PGP-MVS动态择时组合与绩效评价[J]. 运筹与管理, 33(12): 100-107.

10.周亮, 2021. Black-Litterman模型在大类资产配置中的应用：基于货币周期及风险平价策略的改进[J]. 运筹与管理, 30(08): 198-204.

11.周亮, 李红权, 2019. 投资时钟原理及战术资产配置在投资组合管理中的应用——基于修正Black-Litterman模型[J]. 中央财经大学学报(10): 92-105.

12.周亮, 李红权, 2020. 基于马尔科夫区制转换及Black-Litterman模型的大类大类资产配置模型研究[J]. 数理统计与管理, 39(04): 617-632.

13.AI HEDGE FUND. AI hedge fund[EB/OL]. https://github.com/virattt/ai-hedge-fund.

14.ALEXANDER G J, BAPTISTA A M, 2002. Economic implications of using a mean-VaR model for portfolio selection: A comparison with mean-variance analysis[J]. Journal of Economic Dynamics and Control, 26(7-8): 1159-1193.

15.ASNESS C S, 2016. The Siren Song of Factor Timing[J]. SSRN Electronic Journal.

16.ASNESS C S, FRAZZINI A, PEDERSEN L H, 2012. Leverage Aversion and Risk Parity[J]. Financial Analysts Journal, 68(1): 47-59.

17.BASS R, GLADSTONE S, ANG A, 2017. Total Portfolio Factor, Not Just Asset, Allocation[J]. The Journal of Portfolio Management, 43(5): 38-53.

18.BEST M J, GRAUER R R, 1991. On the Sensitivity of Mean-Variance-Efficient Portfolios to Changes in Asset Means: Some Analytical and Computational Results[J]. Review of Financial Studies, 4(2): 315-342.

19.BLACK F, LITTERMAN R, 1992. Global Portfolio Optimization[J]. Financial Analysts Journal, 48(5): 28-43.

20.BRINSON G P, HOOD L R, BEEBOWER G L, 1986. Determinants of Portfolio Performance[J]. Financial Analysts Journal, 42(4): 39-44.

21.BROADIE M, 1993. Computing efficient frontiers using estimated parameters[J]. Annals of Operations Research, 45(1): 21-58.

22.BURGGRAF T, 2021. Beyond risk parity – A machine learning-based hierarchical risk parity approach on cryptocurrencies[J]. Finance Research Letters, 38: 101523.

23.CLARKE R G, DE SILVA H, MURDOCK R, 2005. A factor approach to asset allocation[J]. The Journal of Portfolio Management, 32(1): 10-21.

24.COCHRANE J H, 2011. Presidential address: Discount rates[J]. The Journal of finance, 66(4): 1047-1108.

25.DICHTL H, DROBETZ W, WENDT V, 2021. How to build a factor portfolio: Does the allocation strategy matter?[J]. European Financial Management, 27(1): 20-58.

26.HOOD R L, 2005. Determinants of portfolio performance—20 years later[J]. Financial Analysts Journal, 61(5): 6-8.

27.KO H, LEE J, 2024. Can ChatGPT improve investment decisions? From a portfolio management perspective[J]. Finance Research Letters, 64: 105433.

28.LI C, CHAN C H R, HUANG S H, et al., 2025. Integrating LLM-Based Time Series and Regime Detection with RAG for Adaptive Trading Strategies and Portfolio Management[M]//CHOI P M S, HUANG S H. Finance and Large Language Models. Singapore: Springer Nature Singapore: 129-146.

29.LUO Y, FENG Y, XU J, 等, 2025. LLM-Powered Multi-Agent System for Automated Crypto Portfolio Management[A]. arXiv.

30.MARKOWITZ H, 1952. Portfolio Selection[J]. The Journal of Finance, 7(1): 77.

31.PAPPAS S N, DICKSON J M, 2015. Factor-based investing[J]. Vanguard Research.

32.PEDERSEN L H, FITZGIBBONS S, POMORSKI L, 2021. Responsible investing: The ESG-efficient frontier[J]. Journal of Financial Economics, 142(2): 572-597.

33.QIAN E, 2011. Risk parity and diversification[J]. Journal of Investing, 20(1): 119.

34.QIAN E, others, 2005. Risk parity portfolios: Efficient portfolios through true diversification[J]. Panagora Asset Management, 1(1): 1-10.

35.WOODSIDE-ORIAKHI M, LUCAS C, BEASLEY J E, 2011. Heuristic algorithms for the cardinality constrained efficient frontier[J]. European Journal of Operational Research, 213(3): 538-550.

六、附录

6.1 BL模型推导

6.1.1 市场隐含均衡收益推导

6.1.2 后验分布的推导

6.1.3 最优权重（无约束，可加杠杆、做空）

6.1.4 预算约束最优权重（可做空、无杠杆）

6.2 大类资产年化收益率和波动率

6.3 BL-战略基准-自营版结果

6.3.1 自营版相关结果

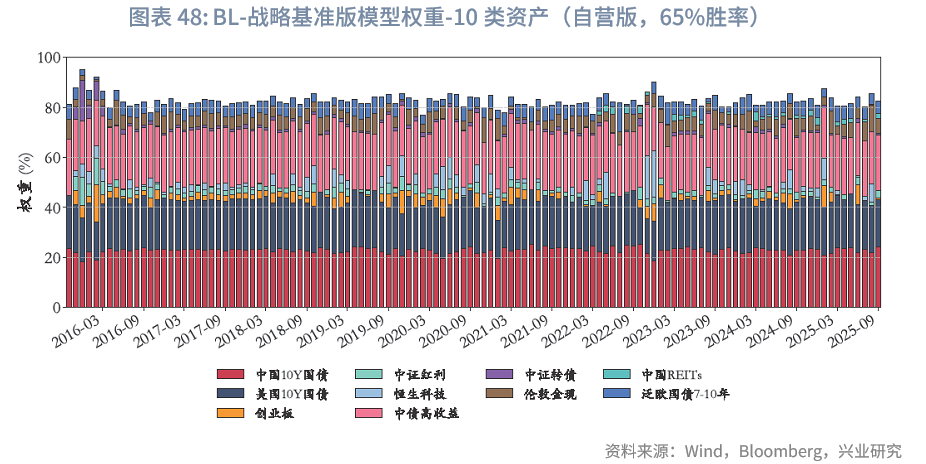
6.4 风险平价模型结果

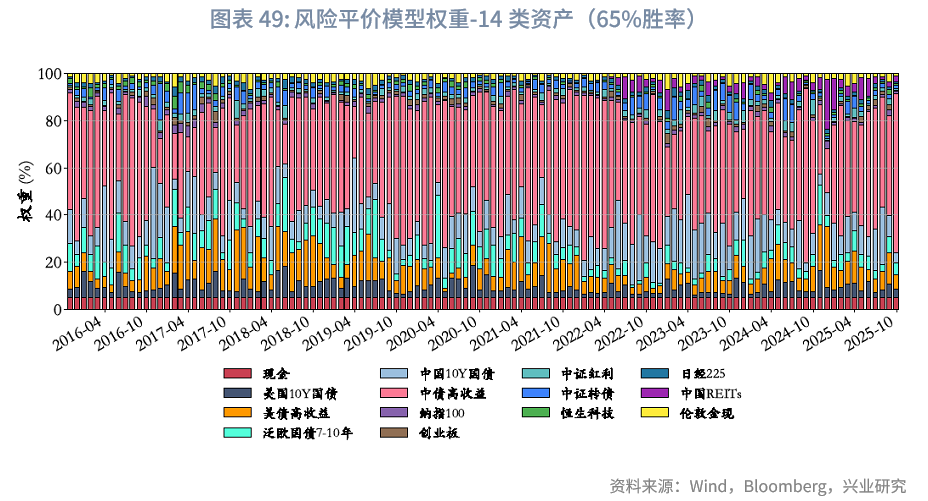
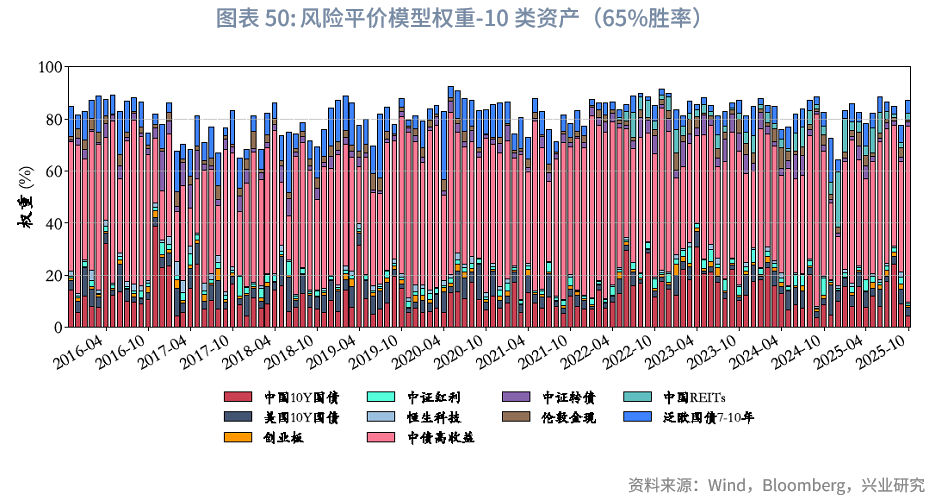
6.4.1 风险平价模型-协方差版相关结果

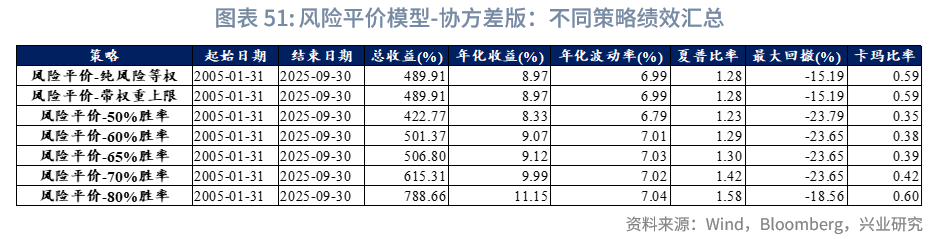
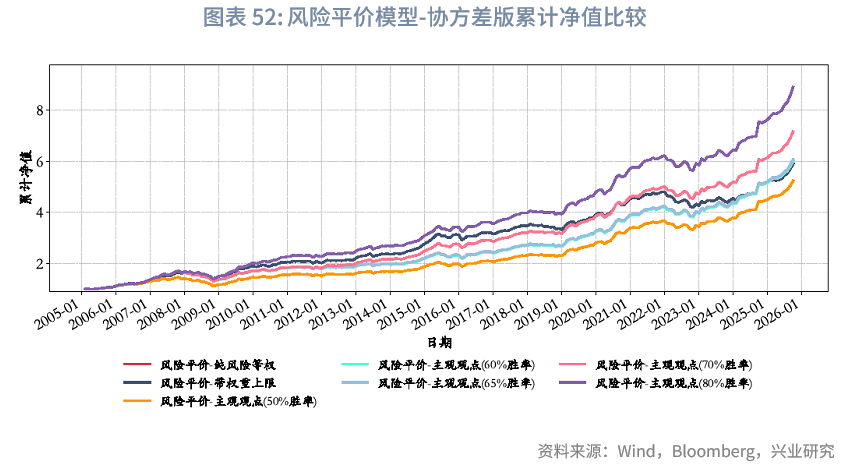
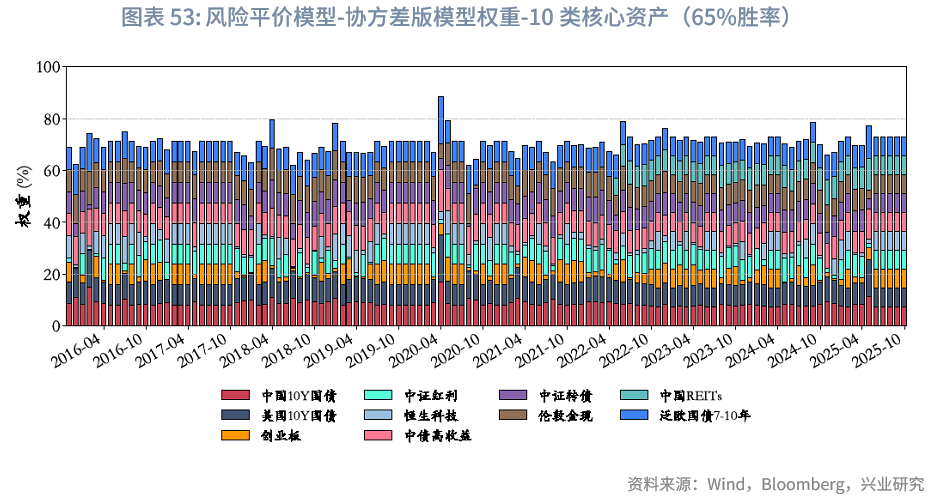
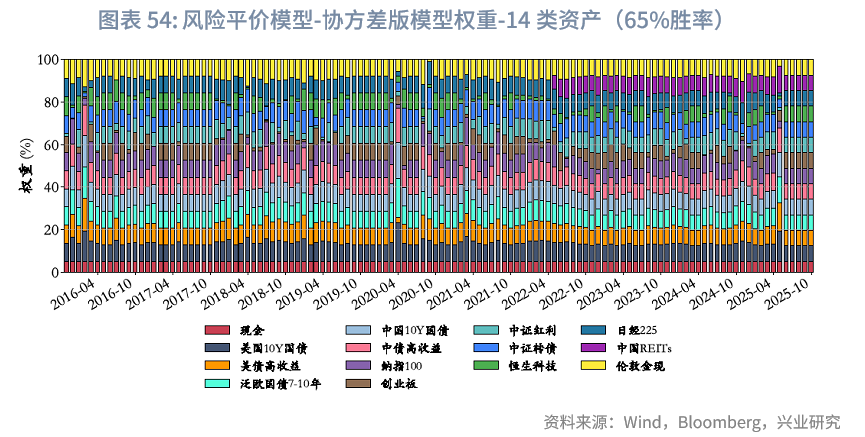
注：

[1]此处“风险平价（无观点）”模型结果与“风险平价模型”中的“纯粹风险等权”版本略有差异，核心原因在于前者需与其余BL模型进行对比——由于BL模型需借助协方差矩阵，因此“风险平价（无观点）”模型假定基于上一年度的日度收益率计算协方差矩阵（2005年全年特殊采用等权重计算）；而单独的“纯粹风险等权”模型，仅需使用上一个月的波动率数据即可。