Adadelta
文章目录
- Adadelta
- Concept
- Equation
- Parameters
- Instance
Adadelta
ADADELTA是一种基于梯度下降的自适应学习率优化算法,由Matthew Zeiler提出。与其他自适应学习率算法(例如Adam和Adagrad)相比,ADADELTA在训练深度神经网络时通常表现更好。
Concept
ADADELTA的核心思想是根据前一次更新时的梯度和参数来自适应地调整学习率。该算法利用了RMSProp的想法,通过对梯度平方的指数移动平均来缩放学习率。与RMSProp不同,ADADELTA使用了一个窗口来存储指数移动平均,并根据该窗口中的值自适应地调整学习率。
Equation
具体地说,给定当前步骤的参数 θt\theta_tθt,和指数移动平均变量 E[g2]tE[g^2]_tE[g2]t 和 E[Δθ2]tE[\Delta\theta^2]_tE[Δθ2]t,其中 ggg 是梯度向量,Δθ\Delta\thetaΔθ 是上一次更新的参数变化量。每次迭代中,计算梯度向量 gtg_tgt,并使用以下公式更新参数:
Δθt=−RMS[Δθ]t−1RMS[g]tgt\Delta \theta_t = - \frac {RMS[\Delta \theta]_{t-1}} {RMS[g]_t} g_t Δθt=−RMS[g]tRMS[Δθ]t−1gt
其中 RMS[x]tRMS[x]_tRMS[x]t 表示变量 xxx 在过去 www 步骤中的平方根均值,这里 www 是一个指定的窗口大小。然后使用以下公式更新指数移动平均变量:
E[g2]t=ρE[g2]t−1+(1−ρ)gt2E[Δθ2]t=ρE[Δθ2]t−1+(1−ρ)Δθt2E[g^2]_t = \rho E[g^2]_{t-1} + (1 - \rho)g_t^2\\ E[\Delta\theta^2]_t = \rho E[\Delta\theta^2]_{t-1} + (1 - \rho) \Delta \theta_t^2 E[g2]t=ρE[g2]t−1+(1−ρ)gt2E[Δθ2]t=ρE[Δθ2]t−1+(1−ρ)Δθt2
其中 ρ\rhoρ 是一个控制指数移动平均的衰减因子,通常设置为0.9。最后,使用以下公式更新参数:
θt+1=θt+Δθt\theta_{t+1} = \theta_t + \Delta \theta_t θt+1=θt+Δθt
Parameters
使用 torch.optim.Adadelta 并设置以下参数:
| 参数 | 描述 | 默认值 |
|---|---|---|
| params (iterable) | 要优化的参数的迭代,或者定义参数组的数据 | 无 |
| rho (float, optional) | 用于计算梯度平方的运行平均值的系数 | 0.9 |
| eps (float, optional) | 添加到分母中以提高数值的稳定性 | 1e-6 |
| lr (float, optional) | 在delta应用于参数之前,对其进行缩放的系数 | 1.0 |
| weight_decay (float, optional) | 权重衰减(L2惩罚) | 0 |
| foreach(bool, optional) | 是否使用优化器的foreach实现 如果用户没有指定(所以foreach为None),我们将尝试使用foreach而不是CUDA上的for-loop实现,因为其性能通常要好很多。 | None |
| maximize(bool, optional) | 根据目标最大化参数,而不是最小化参数 | False |
| differentiable(bool, optional) | 在训练中是否应该通过优化器的步骤发生autograd。否则,step()函数会在torch.no_grad()的背景下运行。设置为True会影响性能,所以如果你不打算通过这个实例运行autograd,就把它设为False。 | False |
Instance
以下是一个使用ADADELTA优化器训练MNIST数据集的示例:
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision.datasets as datasets
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
from torch.utils.data import DataLoader# 定义超参数
learning_rate = 0.1
rho = 0.9
batch_size = 64
num_epochs = 10# 加载MNIST数据集
train_dataset = datasets.MNIST(root='./datasets', train=True, transform=transforms.ToTensor(), download=True)
train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)# 定义模型
class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = nn.Conv2d(1, 32, kernel_size=5)self.conv2 = nn.Conv2d(32, 64, kernel_size=5)self.fc1 = nn.Linear(1024, 512)self.fc2 = nn.Linear(512, 10)def forward(self, x):x = nn.functional.relu(nn.functional.max_pool2d(self.conv1(x), 2))x = nn.functional.relu(nn.functional.max_pool2d(self.conv2(x), 2))x = x.view(-1, 1024)x = nn.functional.relu(self.fc1(x))x = self.fc2(x)return xmodel = Net()# 将模型和数据移动到GPU上
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model.to(device)# 定义优化器
optimizer = optim.Adadelta(model.parameters(), lr=learning_rate, rho=rho)
# 定义损失函数
criterion = nn.CrossEntropyLoss()# 记录损失值
loss_list = []# 训练模型
for epoch in range(num_epochs):total_loss = 0for i, (images, labels) in enumerate(train_loader):# 将数据移动到GPU上images = images.to(device)labels = labels.to(device)# 前向传播outputs = model(images)loss = criterion(outputs, labels)# 反向传播和优化optimizer.zero_grad()loss.backward()optimizer.step()# 记录损失值total_loss += loss.item()# 输出训练信息if (i + 1) % 100 == 0:print('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}'.format(epoch + 1, num_epochs, i + 1, len(train_loader),loss.item())) # 60000/64=937.5# 计算平均损失avg_loss = total_loss / len(train_loader)# 记录平均损失值loss_list.append(avg_loss)# 输出平均损失print('Epoch [{}], Average Loss: {:.4f}'.format(epoch + 1, avg_loss))print('-' * 50)# 绘制loss曲线
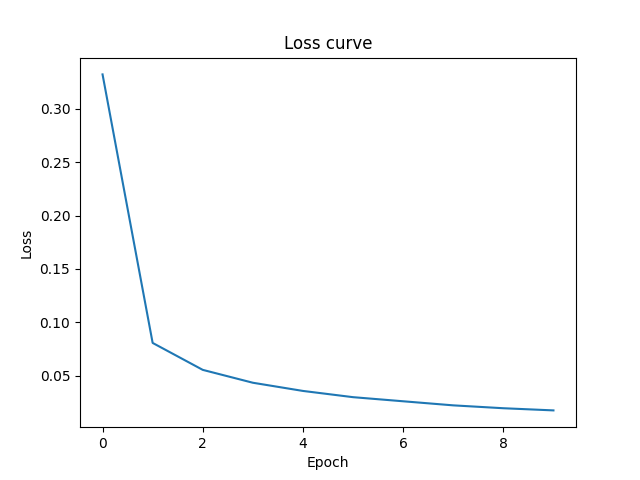
plt.plot(loss_list)
plt.title('Loss curve')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.show()print('Training finished')
Epoch [1/10], Step [100/938], Loss: 0.5616
Epoch [1/10], Step [200/938], Loss: 0.2429
Epoch [1/10], Step [300/938], Loss: 0.3516
Epoch [1/10], Step [400/938], Loss: 0.1991
Epoch [1/10], Step [500/938], Loss: 0.1635
Epoch [1/10], Step [600/938], Loss: 0.1354
Epoch [1/10], Step [700/938], Loss: 0.0416
Epoch [1/10], Step [800/938], Loss: 0.1753
Epoch [1/10], Step [900/938], Loss: 0.0663
Epoch [1], Average Loss: 0.3323
--------------------------------------------------
Epoch [2/10], Step [100/938], Loss: 0.1213
Epoch [2/10], Step [200/938], Loss: 0.0736
Epoch [2/10], Step [300/938], Loss: 0.0663
Epoch [2/10], Step [400/938], Loss: 0.0401
Epoch [2/10], Step [500/938], Loss: 0.0387
Epoch [2/10], Step [600/938], Loss: 0.0682
Epoch [2/10], Step [700/938], Loss: 0.0664
Epoch [2/10], Step [800/938], Loss: 0.0715
Epoch [2/10], Step [900/938], Loss: 0.0153
Epoch [2], Average Loss: 0.0807
--------------------------------------------------
Epoch [3/10], Step [100/938], Loss: 0.0472
Epoch [3/10], Step [200/938], Loss: 0.0277
Epoch [3/10], Step [300/938], Loss: 0.0869
Epoch [3/10], Step [400/938], Loss: 0.0100
Epoch [3/10], Step [500/938], Loss: 0.0275
Epoch [3/10], Step [600/938], Loss: 0.0386
Epoch [3/10], Step [700/938], Loss: 0.1090
Epoch [3/10], Step [800/938], Loss: 0.0356
Epoch [3/10], Step [900/938], Loss: 0.0326
Epoch [3], Average Loss: 0.0555
--------------------------------------------------
Epoch [4/10], Step [100/938], Loss: 0.0106
Epoch [4/10], Step [200/938], Loss: 0.0122
Epoch [4/10], Step [300/938], Loss: 0.0131
Epoch [4/10], Step [400/938], Loss: 0.0655
Epoch [4/10], Step [500/938], Loss: 0.0679
Epoch [4/10], Step [600/938], Loss: 0.0419
Epoch [4/10], Step [700/938], Loss: 0.0761
Epoch [4/10], Step [800/938], Loss: 0.0813
Epoch [4/10], Step [900/938], Loss: 0.0421
Epoch [4], Average Loss: 0.0435
--------------------------------------------------
Epoch [5/10], Step [100/938], Loss: 0.0072
Epoch [5/10], Step [200/938], Loss: 0.0088
Epoch [5/10], Step [300/938], Loss: 0.0490
Epoch [5/10], Step [400/938], Loss: 0.0475
Epoch [5/10], Step [500/938], Loss: 0.0464
Epoch [5/10], Step [600/938], Loss: 0.1294
Epoch [5/10], Step [700/938], Loss: 0.0644
Epoch [5/10], Step [800/938], Loss: 0.0590
Epoch [5/10], Step [900/938], Loss: 0.0601
Epoch [5], Average Loss: 0.0358
--------------------------------------------------
Epoch [6/10], Step [100/938], Loss: 0.0103
Epoch [6/10], Step [200/938], Loss: 0.0198
Epoch [6/10], Step [300/938], Loss: 0.0051
Epoch [6/10], Step [400/938], Loss: 0.0179
Epoch [6/10], Step [500/938], Loss: 0.0788
Epoch [6/10], Step [600/938], Loss: 0.0046
Epoch [6/10], Step [700/938], Loss: 0.0523
Epoch [6/10], Step [800/938], Loss: 0.0980
Epoch [6/10], Step [900/938], Loss: 0.0021
Epoch [6], Average Loss: 0.0299
--------------------------------------------------
Epoch [7/10], Step [100/938], Loss: 0.0758
Epoch [7/10], Step [200/938], Loss: 0.0732
Epoch [7/10], Step [300/938], Loss: 0.0119
Epoch [7/10], Step [400/938], Loss: 0.0706
Epoch [7/10], Step [500/938], Loss: 0.0195
Epoch [7/10], Step [600/938], Loss: 0.0191
Epoch [7/10], Step [700/938], Loss: 0.0357
Epoch [7/10], Step [800/938], Loss: 0.0141
Epoch [7/10], Step [900/938], Loss: 0.0850
Epoch [7], Average Loss: 0.0261
--------------------------------------------------
Epoch [8/10], Step [100/938], Loss: 0.0006
Epoch [8/10], Step [200/938], Loss: 0.0228
Epoch [8/10], Step [300/938], Loss: 0.0172
Epoch [8/10], Step [400/938], Loss: 0.0534
Epoch [8/10], Step [500/938], Loss: 0.0231
Epoch [8/10], Step [600/938], Loss: 0.3439
Epoch [8/10], Step [700/938], Loss: 0.0020
Epoch [8/10], Step [800/938], Loss: 0.0167
Epoch [8/10], Step [900/938], Loss: 0.0198
Epoch [8], Average Loss: 0.0223
--------------------------------------------------
Epoch [9/10], Step [100/938], Loss: 0.0024
Epoch [9/10], Step [200/938], Loss: 0.0035
Epoch [9/10], Step [300/938], Loss: 0.0007
Epoch [9/10], Step [400/938], Loss: 0.0102
Epoch [9/10], Step [500/938], Loss: 0.0089
Epoch [9/10], Step [600/938], Loss: 0.0086
Epoch [9/10], Step [700/938], Loss: 0.0117
Epoch [9/10], Step [800/938], Loss: 0.0251
Epoch [9/10], Step [900/938], Loss: 0.0038
Epoch [9], Average Loss: 0.0196
--------------------------------------------------
Epoch [10/10], Step [100/938], Loss: 0.0042
Epoch [10/10], Step [200/938], Loss: 0.0025
Epoch [10/10], Step [300/938], Loss: 0.0393
Epoch [10/10], Step [400/938], Loss: 0.0002
Epoch [10/10], Step [500/938], Loss: 0.0044
Epoch [10/10], Step [600/938], Loss: 0.0130
Epoch [10/10], Step [700/938], Loss: 0.0318
Epoch [10/10], Step [800/938], Loss: 0.0018
Epoch [10/10], Step [900/938], Loss: 0.0301
Epoch [10], Average Loss: 0.0175
--------------------------------------------------
Training finished