高数重点总结
创始人
2025-05-31 23:47:07

高数

公式不要去死记 配合训练题在训练中记忆

完成一下这些题目

高中函数图像回忆

与其记忆各种公式不如去思考他们的本质
这和调用c++动态库可不一样 考试的时候你相当于在使用汇编答题

1 定义域（x）

性质

  • 1/x(x=!0)
  • √x(x>0 || x=0)
  • log a x (x>0)

有界

f(x)=sinx 1/x,[-1,1]

2 奇偶性

  • 偶 f(-x)=f(x)
  • 奇 f(-x)=-f(x)
  • 例题
  • f(x)=ln[x+√ (x^2+1)] 判断奇 偶
    • 解 :f(-x)=ln[√(x^2 +1) -x] -->分子有理化 (x2+1)-x2 / √(x^2+1) + x
      =ln 1 / √(x^2+1) + x ----> ln x ^-1 = -ln x
      =…奇
  • 例二
    • y=f(x)+f(-x) 偶
    • y=f(x)-f(-x) 奇
  • 例三
    • sin tan cot 奇
    • cos 偶
  • #define 奇 0
  • #define 偶 1
    • 0+0=0 1+1=1 1+0 啥也不是
    • 0×0=1 1×1=1 0×1=0
  • ∫a -a f(x)dx
    • f(x)奇 =0
    • 偶 =2倍本身

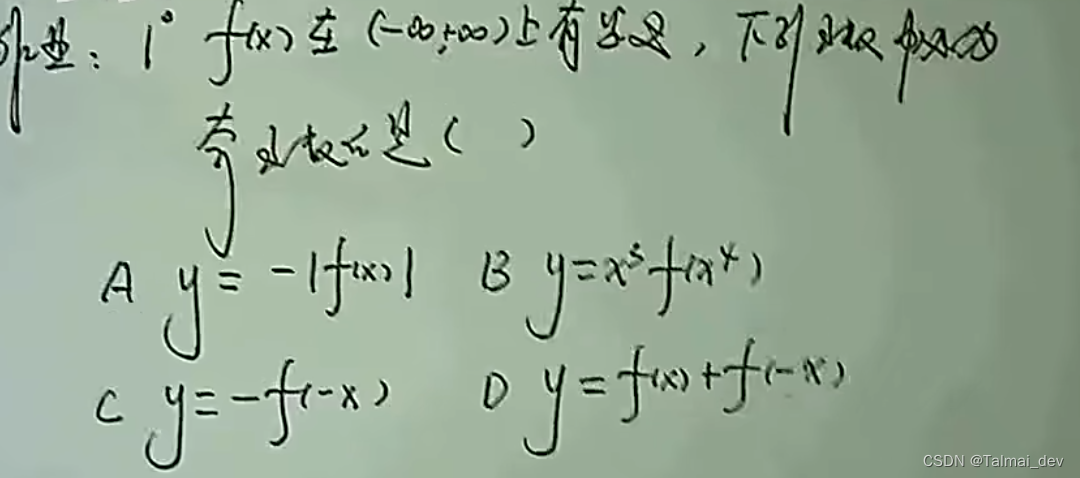
在这里插入图片描述
在这里插入图片描述

1 简单的三个三角函数图像以及性质

三角函数性质

id象限
sin+ + - -
con+ - - +
tan+ - + -
cot=1/tan+ - + -
sec=1/cos+ - - +
csc=1/sin+ + - -

两角和差

sin(A+B)= sinA cosB + cosA sinB
cos(A+B)=cosAcosB +sinAsinB
tan(A+B)=(tanA-tanB)/(1-tanAtanB)
cot(A+B)=(cotAcotB-1)/(cotB+cotA)

倍角公式

二倍

tan2A =2tanA/(1-tan^2 A)

sin2A =sin2sinAcosA

cos2A =cos^2 A - sin^2 A

必备三角函数求导公式

正弦函数 (sinx)‘=cosx
余弦函数：(cosx)’=-sinx
正切 (tanx)‘=sec2x
余切 (cscx)’=cotx*cscx

极限

在这里插入图片描述

重要极限

在这里插入图片描述

等价无穷小转换（无理由直接转）

常用转换x
sin x~x
tan x~x
arcsin x~x
arctan x~x
ln(1+x)~x
(1+bx)^a -1~ abx
1-cosx ~ (x^2)/2
tanx -sinx~(x^3)/2
e^x -1 ~x

高阶无穷小

连续性

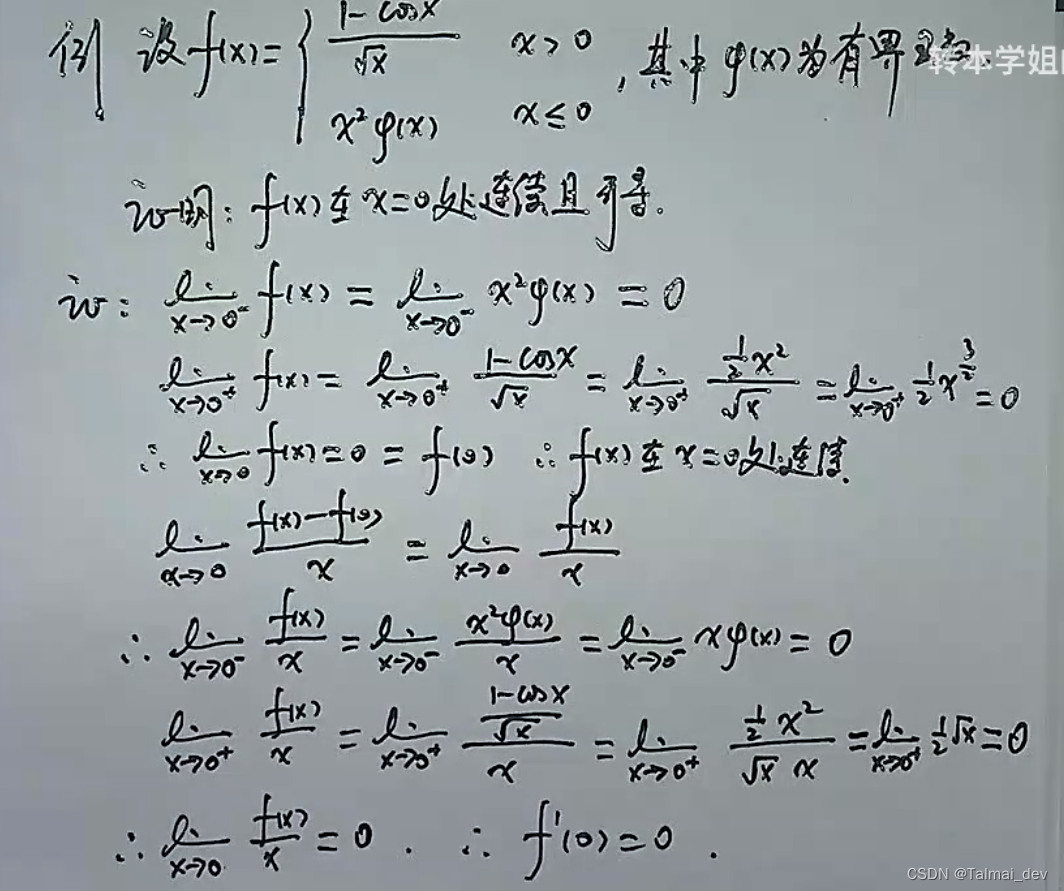
在这里插入图片描述

零点 根存在原理

在这里插入图片描述

连续

在这里插入图片描述

细节性质

驻点 ：函数的一阶导数为零

极值点：极值点是函数图像的某段子区间内上极大值或者极小值点的横坐标。 极值点出现在函数的驻点（导数为0的点）或不可导点处（导函数不存在，也可以取得极值，此时驻点不存在）

可导 -> 极值点一定是驻点

拐点 左右凹凸性变化点

渐进线

在这里插入图片描述

泰勒公式
例题

训练

答案：

-1/2x^2 这一步会出现四次 直接放在最后归于0 o(x)

积分
来一个简单的公式玩一玩

导数 and 微分
##全微分
例1 复合

例2 抽象复合

练习1

例2 多元隐函数

操作

固定公式

同理 阿尔法y替换掉x算出第二个

第三个 d z （这是全微分）
（0，0）表示x=0，y=0
z^3=1
z=1
第一个加第二个

细节
f(x)=f(x)’
f(1)!=f(1)’ 所以这种情况全加‘’‘’‘’‘’‘’导数符号
##二重积分
####概念 性质 计算

导数

原函数导
( c)'=0
(x^n)’ = nx^n-1
(sin x)'=cosx
(cos x)'=-sinx
(tan x)'=sec^2 x
(cot x)‘’=-csc^2 x
(sec x)'= sec x tan x
(csc x)'= - csc x cot x
(a^x)’ = a^x lna
(log a x)'=1/ x lna

(arcsin x)’ =1/ √ (1-x^2)
(arccos x)‘= -1/ √ (1-x^2)
(arctan x)’ = 1/(1+x^2)
(arccot x)'= -1/(1+x^2)

积分

----|-------
∫kdx=kx+C

词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。

上一篇：手动创建数据集（csv文件），用于Pytorch深度学习

下一篇：第一章 信息化知识

相关内容

热门资讯

财经时评｜以创新厚度重塑汽车产... 作者 远山中国汽车工业协会与工业和信息化部近期针对行业“内卷式”竞争的联合发声，为持续蔓延的价格战按...
恒生指数午盘下跌2.20%，恒... 6月2日午盘，香港恒生指数下跌2.20%，报22778.45点；恒生科技指数下跌2.43%，报504...
“以旧换新”带货1万亿，中国何... “美国想让制造业回流成为中国的样子，一个踏实劳作的‘生产者社会’；而中国想努力扩大消费成为美国的样子...
恒指半日跌2.2% 恒指半日跌... 【恒指半日跌2.2%】截至午间收盘，香港恒生指数下跌2.20%，报22778.45点；恒生科技指数下...
“成分之争”舆论战升级，巨子生... 重组胶原蛋白成分之争的舆论战再度升级。美妆博主 "大嘴博士" （郝宇）近日连续发文质疑，巨子生物（0...
汇川技术新注册《InoCube... 证券之星消息，近日汇川技术（300124）新注册了《InoCube-InoData数据分析系统V1....
八旬老人花105万买基金亏了3...
博将控股多家所投企业荣登202... 博将控股多家所投企业荣登2025杭州独角兽与准独角兽榜单 2025年4月24日，由民建浙江省委会、浙...
刚刚，A50直线跳水！亚太股市... 6月2日，亚太股市开盘后持续走弱。富时中国A50期货开盘跌0.6%，截至目前跌幅1.91%。 截至...
问界、智界、享界、尊界，202... 2025鸿蒙智行：四界表现鸿蒙智行作为国内造车新势力的主流品牌，一共规划了“五界”车型，包括：问界、...
花样年控股：重组支持协议的最后... 6月1日，花样年控股（01777.HK）公告称，公司2024年4月29日所订立的重组支持协议的最终截...
蜜雪集团股价创上市以来新高 蜜... 新京报贝壳财经讯 6月2日，港股蜜雪集团盘中涨超7%，股价刷新上市新高。
美单边关税让全球经济面临更大不... 美国征收关税的对象和标准可能随意变更，其关税政策具有不可预测性。无论是外国企业，还是美国本土企业，都...
桃李面包创始人向其两儿子转让3... 5月30日晚间，桃李面包（沪市代码：603866）公告称，公司控股股东及实际控制人吴志刚通过大宗交易...
前4月东莞重大项目完成投资42... 本期看点：前4月东莞重大项目完成投资429.09亿元；长联科技募投项目提升年产至2.77万吨；广东省...
恒生指数跌幅扩大至2%，医药、... 6月2日，恒生指数跌幅扩大至2%，医药、地产、能源板块跌幅居前，美中嘉和跌超14%，石四药集团跌近1...
港股、A50飘绿，亚太市场多数... 早间，亚太市场多数下跌。港股、A50集体下跌其中，恒生指数、恒生科技指数开盘跌幅扩大， 港股生物技术...
雷军看好的两兄弟，要IPO了 ... 2021年夏，小米产业园办公室内，雷军饶有兴致地打量眼前一对兄弟，“为什么张波是创始人，董事长却是张...
圣阳股份涨1.66%，成交额9... 5月30日，圣阳股份涨1.66%，成交额9.82亿元，换手率15.03%，总市值66.67亿元。 异...
“龙舟溪游”点燃江南西商圈消费... 5月31日至6月2日，海珠区江南中街道一年一度的节假日消费体验活动如约而至。今年“龙舟溪游・与你童在...
恒生指数开盘跌1.06%，恒生... 6月2日，恒生指数开盘跌1.06%报23043.10点，恒生科技指数跌1.33%，恒生中国企业指数跌...
*ST天喻实控人被刑事立案 此... 5月30日，*ST天喻（300205.SZ）发布公告称，公司收到武汉市公安局送达的《立案告知书》，公...
“玩”出更多花样——“六一”礼... 能交流、讲故事的毛绒玩偶，融入中国文化、科技元素的拼插积木，电影《哪吒2》衍生开发的各类公仔……“六...
5月十大牛股出炉：中邮科技逾1... 截至5月30日收盘，沪指月内累计涨2.09%，深证成指累计涨1.42%，创业板指累计涨2.32%。在...
恒生指数止步周线七连阳，IPO... 南方财经全媒体记者 袁思杰 实习生武桐羽 香港报道上周（5月26日-5月30日），港股震荡回调，主要...
新势力车企5月放榜：零跑汽车登... 近期，国内多家主流自主汽车企业纷纷发布了5月份的销售数据。造车新势力5月交付成绩也出炉，第一名依然是...
最新！2025新势力5月销量出... 5月新势力表现如何？2025年5月的销售周期刚刚过去，不少造车新势力厂商的销量数据，已经新鲜出炉。数...
两家A股公司，收终止上市决定 又有两家A股上市公司收到股票终止上市决定，6月10日进入退市整理期。 上述自律监管决定书指出，因2...
重磅，事关教育强国，主力提前埋... 数据是个宝数据宝投资少烦恼这些产业的景气度处于上升期。《求是》杂志发表文章《加快建设教育强国》6月1...
阳光诺和“二刷”收购 80后富... 《投资者网》蔡俊时隔2年后，阳光诺和（688621.SH，下称“公司”）再拟收购同一个资产。实际上，...