原文链接：https://ieeexplore.ieee.org/document/9156568

1. 引言

  本文提出点云的一种新表达，它封装了点云的局部信息，且对坐标系变换、缩放和排列具有鲁棒性。如下图所示，其关键思想是将点云实例的隐式函数嵌入神经网络中，并将神经网络的权重作为点云的特征。

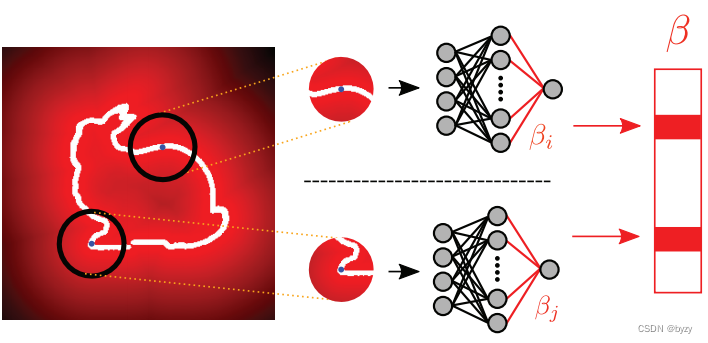
  首先将点云转换为隐式函数，即距离场。通过将固定采样点数的“采样球”(图中黑色圆圈)放置在每一个点上来获取距离场。每个采样球的距离场均被嵌入一个神经网络，使得隐式表达具有排列不变性。所有网络的权重（图中βi\beta_iβi​）被拼接为矩阵，作为点云的表达。使用极端学习机（ELM）来嵌入距离场，以比较不同实例的网络权重。
  该表达由局部嵌入网络的权重组成，通过改变网络成分并对齐距离场，可对坐标变换和缩放具有不变性。尺度不变性是通过ELM的ReLU激活函数实现的；坐标不变性则是通过使用采样点的标准坐标实现的，这一标准坐标是通过将标准空间（由每个实例的距离值分布决定）与距离场对齐得到的。
  本文提出的点云表达只需要简单的神经网络，因此可以减少训练时间。

3. 方法

  本文的方法包含两个步骤：点云到隐式表达（即距离场）的转换以及隐式表达的网络嵌入。

3.1 隐式表达：距离场

  选择距离场作为隐式表达的原因有两点：距离场具有点的排列不变性、距离是与尺度协同变化的（能实现表达的尺度不变性）。
  给出由nnn个表面点p∈R3p\in \mathbb{R}^3p∈R3组成的点云PPP，采样点x∈Xx\in Xx∈X在周围空间内的距离函数ϕ\phiϕ被定义为ϕ(x)=min⁡p∈P∣∣x−p∣∣\phi(x)=\min_{p\in P}||x-p||ϕ(x)=p∈Pmin​∣∣x−p∣∣  实际中，本文将采样球放置在点云PPP的每一个表面点上，每个采样球内包含mmm个采样点xxx，这mmm个采样点xxx在所有点云实例采样球中的位置是相同的。球内采样点的坐标被归一化为相对球心的坐标，从而归一化球内的距离函数为ϕPi(x)=min⁡p~∣∣xi−p~∣∣\phi_{P_i}(x)=\min_{\tilde{p}}||x_i-\tilde{p}||ϕPi​​(x)=p~​min​∣∣xi​−p~​∣∣其中p~=p−pi\tilde{p}=p-p_ip~​=p−pi​是表面点相对于第iii个表面点pip_ipi​（即球心）的归一化坐标。
  在采样球和目标形状被旋转后，采样点的坐标改变了，但球内的距离场保持不变。
  采样球的半径与包含整个点云的球的半径相关。若形状是局部的或是开放的，则假设点云密度均匀，将采样球的半径定义为每个点到其kkk近邻点的距离均值。

3.2 隐式表达的参数化

  对每个表面点ppp，将其距离场嵌入神经网络，从而使网络权重能够捕捉采样球内的距离信息。常规的神经网络可以进行多种权值组合（各层权重同时被优化）。为进行权重比较，需要将它们嵌入到相同的度量空间中，因此本文使用极端学习机（ELM）。

简单来说，极端学习机就是特殊的前馈网络，不同之处在于：

1. 仅需优化最后隐藏层到输出层的权重，其余权重可随机设置并在训练时固定；
2. 隐藏层到输出层的权重通过解析计算确定，而非迭代优化。

因此，实际上ELM在训练和测试过程中就表现为一个固定的函数。

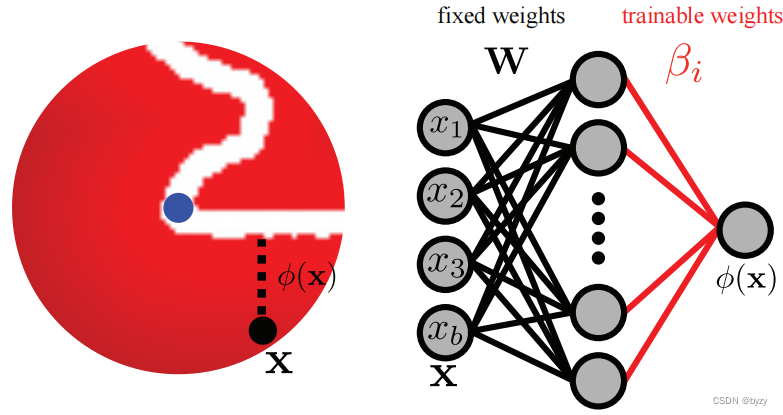
  本文使用3层的ELM，其中输入层到隐藏层的权重被固定为WWW（如上右图所示），仅优化隐藏层到输出层的权重β\betaβ。ELM的输入为采样点到球心表面点的归一化位置X∈Rm×3X\in\mathbb{R}^{m\times3}X∈Rm×3；ELM的训练目标是返回采样点到点云PPP中最近点的距离ΦPi(X)\Phi_{P_i}(X)ΦPi​​(X)（如上左图所示），目标函数为：βi∗=arg min⁡βi∣∣ΦPi(X)−βiTf(WXT+b)∣∣F2\beta^\ast_i=\argmin_{\beta_i}||\Phi_{P_i}(X)-\beta_i^Tf(WX^T+b)||_F^2βi∗​=βi​argmin​∣∣ΦPi​​(X)−βiT​f(WXT+b)∣∣F2​其中fff是非线性激活函数，W∈Rk×3W\in\mathbb{R}^{k\times3}W∈Rk×3和b∈Rkb\in\mathbb{R}^kb∈Rk是随机权重和偏置。为求取权重β\betaβ，仅需求取H=f(WX+b)H=f(WX+b)H=f(WX+b)的伪逆，得到β∗=H†ΦP(X)\beta^\ast=H^\dagger\Phi_P(X)β∗=H†ΦP​(X)，或更鲁棒地，得到βi∗=(cI+HTH)−1HTΦPi(X)\beta_i^\ast=(cI+H^TH)^{-1}H^T\Phi_{P_i}(X)βi∗​=(cI+HTH)−1HTΦPi​​(X)其中ccc为常数，为反应尺度，将其设置为采样点XXX的方差。这样可以得到与XXX的排列顺序无关的唯一解β∗\beta^\astβ∗。
  本文将所有ELM的WWW固定为相同的正交随机矩阵，则权重β\betaβ由距离场决定。利用ELM的这一特性，每个采样球能得到唯一的权值β\betaβ。

3.2.1 固定WWW

  固定WWW的原因除了前面提到的固定权重β\betaβ的度量空间以外，还能提高计算效率。因为采样点在采样球内的位置是固定的，即XXX固定，则当WWW固定时，H=f(WX+b)H=f(WX+b)H=f(WX+b)及其伪逆(cI+HTH)−1HT(cI+H^TH)^{-1}H^T(cI+HTH)−1HT在整个数据集中均只需要计算一次，而非对每个采样球单独计算。
  为了同时计算所有采样球对应的拼接权重β\betaβ，需要将各采样球的距离场拼接为矩阵，从而β∗=(cI+HTH)−1HTΦP(X)\beta^\ast=(cI+H^TH)^{-1}H^T\Phi_P(X)β∗=(cI+HTH)−1HTΦP​(X)其中ΦP(X)∈Rm×n\Phi_P(X)\in\mathbb{R}^{m\times n}ΦP​(X)∈Rm×n，β∗∈Rk×n\beta^\ast\in\mathbb{R}^{k\times n}β∗∈Rk×n，nnn为采样球的数量。

3.3 实现坐标和尺度不变性

  可以通过修改ELM的输入和激活函数来使ELM权重β\betaβ具有坐标和尺度不变性。

3.3.1 坐标不变性：标准投影

  本文将距离场投影到4D规范空间上，以实现旋转不变性。引入采样矩阵X=[x1,x2,⋯,xm]T∈Rm×3X=[x_1,x_2,\cdots,x_m]^T\in\mathbb{R}^{m\times3}X=[x1​,x2​,⋯,xm​]T∈Rm×3和对应的采样距离向量ΦP(X)=[ϕ(x1),ϕ(x2),⋯,ϕ(xm)]T∈Rm\Phi_P(X)=[\phi(x_1),\phi(x_2),\cdots,\phi(x_m)]^T\in \mathbb{R}^mΦP​(X)=[ϕ(x1​),ϕ(x2​),⋯,ϕ(xm​)]T∈Rm，拼接为M=[X,ΦP(X)]M=[X,\Phi_P(X)]M=[X,ΦP​(X)]。对MMM使用奇异值分解（SVD）得到M=USVTM=USV^TM=USVT  由于SVD的结果存在符号模糊性，本文使用所有符号排列来转换数据。准备一个元素均为1或-1的向量ccc，以其为对角线构造对角矩阵CCC，记VˉT=VTC\bar{V}^T=V^TCVˉT=VTC。
  若令Mˉ=MVˉ\bar{M}=M\bar{V}Mˉ=MVˉ，其中Vˉ\bar{V}Vˉ是将数据矩阵投影到4维规范空间的矩阵。该投影根据距离场的方差将距离场对齐到唯一的姿态上，如下图所示。

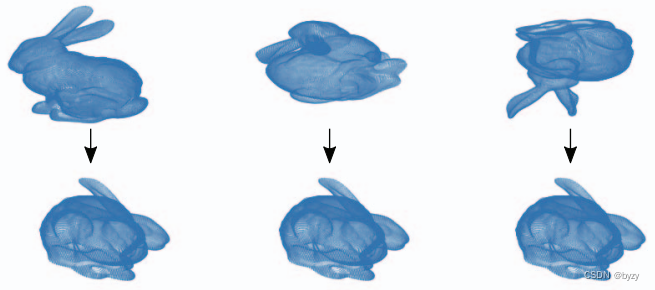
  本文使用所有可能的符号排列来解决符号模糊的问题。ELM的输入为Xˉ=XVˉx\bar{X}=X\bar{V}_xXˉ=XVˉx​（其中Vˉx∈R3×4\bar{V}_x\in\mathbb{R}^{3\times4}Vˉx​∈R3×4为Vˉ\bar{V}Vˉ的前3行），即采样点投影到4D规范空间中的坐标。输入中移除了距离向量来避免平凡解。
  为高效求取Vˉx\bar{V}_xVˉx​，本文放置一个包含整个点云实例的全局球体，用于对齐全局距离场到一个唯一的姿态。对齐后再在表面点上放置采样球。

3.3.2 尺度不变性：ReLU激活函数

  本文利用ReLU函数的尺度可交换性（即ReLU(sx)=sReLU(x)\text{ReLU}(sx)=s\text{ReLU}(x)ReLU(sx)=sReLU(x)）实现尺度不变性。通过移除3.2节第一式中的偏置项bbb并令f=ReLUf=\text{ReLU}f=ReLU，可得：β∗=arg min⁡β∣∣ΦP(X)−βTf(WXˉb)∣∣F2\beta^\ast=\argmin_{\beta}||\Phi_{P}(X)-\beta^Tf(W\bar{X}_b)||_F^2β∗=βargmin​∣∣ΦP​(X)−βTf(WXˉb​)∣∣F2​其中Xˉb∈Rm×(4+1)\bar{X}_b\in\mathbb{R}^{m\times(4+1)}Xˉb​∈Rm×(4+1)为添加1列偏置的Xˉ\bar{X}Xˉ，该偏置是通过计算Xˉ\bar{X}Xˉ各值的标准差得到的。
  下面证明尺度不变性。假设输入Xˉb\bar{X}_bXˉb​的缩放因数为sss（相应缩放ΦP(X)\Phi_P(X)ΦP​(X)），故上式近似为sΦP(X)≈β∗Tf(WsXˉb)=sβ∗Tf(WXˉb)s\Phi_P(X)\approx\beta^{\ast T}f(Ws\bar{X}_b)=s\beta^{\ast T}f(W\bar{X}_b)sΦP​(X)≈β∗Tf(WsXˉb​)=sβ∗Tf(WXˉb​)消去等式两端的sss可知网络权重β∗\beta^\astβ∗不变。其它满足尺度可交换性的函数也可作为本文的激活函数。

4.实验

  网络结构类似PointNet，如下图所示。

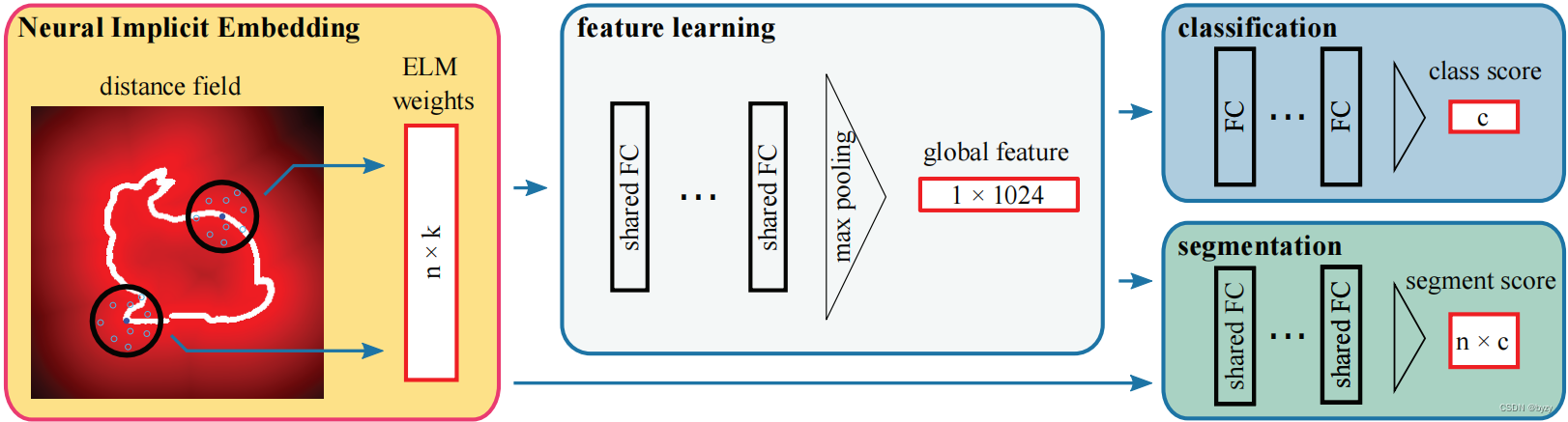
4.1 分类精度

  本文使用ModelNet10/40数据集。为和其余方法公平比较，首先将CAD模型归一化为0均值并包含在单位球内，再均匀采样固定数量的表面点。然后为每个表面点准备一个采样球并训练一个ELM，将数据转换为ELM的权重。
  实验表明本文的方法在所有基于点云的方法中表现很好。为点的特征附加法向量和点的坐标能提升性能，但不再有尺度不变性。
  添加噪声作为通常的数据增广方式，在本文方法中会带来性能下降，这可能是由于ELM的使用已经包含了一定的误差，与为点云添加噪声是等价的。

4.2 相关元素对嵌入的影响

  分别改变ELM权重WWW的维度kkk，采样球的半径和采样点的数量mmm进行实验：当三个值均很小时性能较差，但增大它们会使性能先达到峰值，然后略微下降。这可能是因为节点很少的ELM不能捕捉太多的信息。
  此外，注意到本文的模型很简单，能够大幅降低训练时间。

4.3 对表面点数量的鲁棒性

  将点云进行子集采样进行实验，性能仅略有下降，表明距离场对原始点云密度的鲁棒性。

4.4 规范嵌入的影响

  训练集不适用数据增广，对测试集进行随机旋转：实验表明增大旋转角度会使其余方法有严重的性能下降，而本文方法仅因为旋转带来的采样噪声而性能略有下降。若在训练时使用随机旋转数据增广，其余方法仅有很小的性能提升，因为物体姿态有无穷多种。进一步对测试数据进行缩放，其余方法的性能会进一步下降，而本文方法能保持性能。

4.5 点云分割

  使用ShapeNetCore Part数据集。分割头的输入为ELM权重与池化后的全局特征相拼接的结果。
  与基于PointNet的系列方法相比，本文方法有最高的mIoU。注意本文提出的表达可与点云坐标拼接，因此可以直接插入许多复杂模型。

5. 结论

  本文的模型训练分两步：第一步是ELM的无监督训练（生成距离场作为监督）；第二步是具体任务相关模型的训练（常规训练方法）。注意测试数据也会进行第一步训练。
  之前的许多方法未考虑旋转不变性，会在重力方向未知时失效。此外本文的方法无需通过数据增广考虑物体各种可能的姿态，而是将形状信息处理到一个统一的参数空间中。