机器学习的模型评估
模型评估
模型分为分类模型 和回归模型
模型简介
| 类别 | 评估方法 | 简介 |
|---|---|---|
| 分类模型 | 准确率(Accuracy) | 预测正确的样本数占总样本数的比例 |
| 精确率(Precision) | 预测为正例的样本中实际为正例的比例 | |
| 召回率(Recall) | 实际为正例的样本中被预测为正例的比例 | |
| F1-Score | 精确率和召回率的调和平均数 | |
| ROC曲线和AUC值 | 用于衡量二分类模型的性能,AUC值越接近1,分类器性能越好 | |
| PR曲线和AP值 | 用于衡量二分类模型的性能,AP值越接近1,分类器性能越好 | |
| 混淆矩阵(Confusion Matrix) | 用于展示分类器分类结果的统计表格 | |
| 回归模型 | 均方误差(MSE) | 预测值与真实值之间差值的平方和的平均值 |
| 均方根误差(RMSE) | MSE 的平方根 | |
| 平均绝对误差(MAE) | 预测值与真实值之间差值的绝对值的平均值 | |
| R²(R-Squared) | 回归模型的拟合优度评估方法,取值范围0到1,越接近1代表模型的拟合效果越好 | |
| 相对平均误差(RAE) | MAE 的一种标准化指标,表示预测值与真实值之间差值的平均值占真实值的比例 | |
| 相对平方误差(RSE) | MSE 的一种标准化指标,表示预测值与真实值之间差值的平方和占真实值平方和的比例 | |
| 交叉验证 | 将数据集分为训练集和测试集,用于评估模型性能的方法,包括K折交叉验证和留一交叉验证 |
模型优缺点:
假正例(False Positive,FP)
是指在分类预测中,
某个样本实际上属于负例(反例),
但被模型预测成了正例(正例)。
简单来说,就是原本应该判断为负的样本,
却被错误地判断为正的情况。
| 评估方法 | 优点 | 缺点 |
|---|---|---|
| 准确率(Accuracy) | 直观、易于理解,适用于类别均衡的情况 | 对于类别不平衡的数据,准确率可能无法反映模型的真实性能 |
| 精确率(Precision) | 关注预测为正例的样本中实际为正例的比例,适用于关注假正例的场景 | 不关注假反例,可能在某些场景中不够全面 |
| 召回率(Recall) | 关注实际为正例的样本中被预测为正例的比例,适用于关注假反例的场景 | 不关注假正例,可能在某些场景中不够全面 |
| F1-Score | 综合考虑精确率和召回率,适用于关注精确率和召回率平衡的场景 | 可能无法充分反映某些关注特定类别或特定性能的场景需求 |
| ROC曲线和AUC值 | 不受类别不平衡影响,适用于衡量二分类模型的性能 | 仅适用于二分类问题 |
| PR曲线和AP值 | 考虑了精确率和召回率,适用于衡量二分类模型的性能 | 仅适用于二分类问题 |
| 混淆矩阵(Confusion Matrix) | 直观地展示分类器在各个类别上的表现,便于计算各种评价指标 | 可能无法直观地反映整体模型性能 |
| 均方误差(MSE) | 易于理解,适用于衡量回归模型的预测误差 | 对异常值敏感,可能无法反映真实的预测效果 |
| 均方根误差(RMSE) | 易于理解,与预测值同一量级,适用于衡量回归模型的预测误差 | 对异常值敏感,可能无法反映真实的预测效果 |
| 平均绝对误差(MAE) | 易于理解,对异常值不敏感,适用于衡量回归模型的预测误差 | 由于对异常值不敏感,在某些场景下可能不符合实际需求 |
| R²(R-Squared) | 反映了模型的拟合优度,取值范围0到1,越接近1代表模型的拟合效果越好 | 对异常值敏感,可能无法充分反映真实的拟合效果 |
| 相对平均误差(RAE) | 考虑了预测误差相对于真实值的比例,适用于衡量回归模型的预测误差 | 可能受到不同数据集或量纲影响,难以进行不同模型的比较 |
| 相对平方误差(RSE) | 考虑了预测误差的平方和相对于真实值平方和的比例,适用于衡量回归模型的预测误差 | 考虑了预测误差的平方和相对于真实值平方和的比例,适用于衡量回归模型的预测误差 |
| 交叉验证 | 通过将数据集分为训练集和测试集评估模型性能,能够更好地评估模型在未知数据上的表现 | 计算成本较高,对于大型数据集可能需要较长的计算时间 |
思考
思考1:
对异常值敏感不敏感就是平方不平方吗?
不完全是。异常值对评估指标的影响程度与评估方法中所涉及的计算公式有关,而不仅仅是平方与否的问题。
确实,平方误差(如均方误差MSE和均方根误差RMSE)中的平方操作会放大预测误差,因此它们对异常值较为敏感。但是,有些其他评估指标也可能对异常值敏感,即使它们并不涉及平方操作。
平均绝对误差(MAE)是一个不涉及平方操作的评估指标,它对异常值相对不敏感。MAE使用绝对值来衡量预测值与真实值之间的误差,因此不会像平方误差那样放大异常值造成的影响。
总的来说,评估指标对异常值的敏感程度取决于评估方法中的计算公式,而非单纯地看其是否涉及平方操作。
思考2:
评估算法的优劣性,也就说算法的优缺点,以及算法之间的区分度,是在于他覆盖的范围全不全面,对异常值敏感不敏感。还有其他的吗?
··评估算法的优劣性(优缺点)和区分度主要取决于以下几个方面:
覆盖范围:好的评估指标能够全面地评估模型在不同情况下的性能,包括对不同类型的错误和预测表现的评估`。
对异常值的敏感性:有些评估指标对异常值敏感,可能会放大异常值的影响,导致评估结果偏离实际表现。对异常值不敏感的评估指标能够更好地反映模型在大多数情况下的性能。
可解释性:优秀的评估指标应该具有较好的可解释性,能够直观地反映模型的性能,便于分析和理解。
稳定性:优秀的评估指标应具有较好的稳定性,即在不同的数据集、模型和环境下能够保持一致的评价标准。
可比较性:在评估多个模型时,需要能够方便地进行性能比较。一个好的评估指标应该能够提供可比较的评价结果,以便于分析和选择最佳模型。
误差偏差和方差:
| 类别 | 定义 | 描述 |
|---|---|---|
| 误差 | 预测值与真实值之间的差距 | 训练误差:模型在训练集上的表现;测试误差:模型在测试集上的表现。误差越大,模型的预测能力越弱。 |
| 偏差 | 模型预测值的期望与真实值之间的差距 | 偏差越大,模型越难以拟合真实数据。 |
| 方差 | 模型预测值的离散程度 | 方差越大,模型对训练集的过拟合程度越高,容易受到噪声的影响。 |
联系 误差可以分解为偏差和方差的和 减小偏差或方差或二者兼顾可以降低误差。在实践中,需要找到一个偏差-方差均衡点。
方差 = Σ(数据 - 均值)² / 数据数量
疑问?
预测值与真实值之间的差距,模型预测值的期望与真实值之间的差距这两个有区别吗,我不太理解?
预测值与真实值之间的差距关注的是单个数据点的预测能力,而模型预测值的期望与真实值之间的差距关注的是模型在整体上的拟合能力。
经验误差和泛化误差
经验误差指模型在训练数据上的表现,衡量模型拟合能力。泛化误差指模型在新数据上的表现,衡量模型实际性能。好的模型需具备低经验误差和泛化误差,平衡训练与测试数据表现,以达到较好泛化能力。
过拟合和欠拟合:
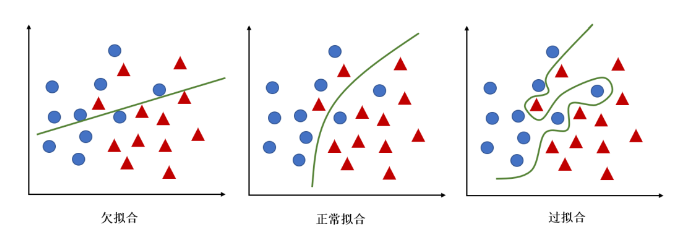
欠拟合:当模型过于简单时,无法很好地捕捉到数据的潜在规律,这时模型在训练集和测试集上都可能具有较高的误差。这种情况下,模型的偏差较大,因为模型的预测值与真实值之间存在较大的差距。欠拟合的模型通常具有较低的方差,因为简单的模型对训练集的变化不敏感,不容易受到噪声的影响。
过拟合:当模型过于复杂时,可能在训练集上表现得非常好,但在测试集上表现较差。这种情况下,模型的方差较大,因为复杂的模型对训练集的变化非常敏感,容易受到噪声的影响。过拟合的模型通常具有较低的偏差,因为它们能够很好地拟合训练集,预测值与真实值之间的差距较小。
过拟合的分类方法看起来很好,实际上再测试集表现很差,而且如此陡峭的曲线,如果出现一个很平常的误差,因为曲线太抖了,再加上方差平方的加持,就会显示出误差很大,就会导致整体的方差较大【要结合图来分析】
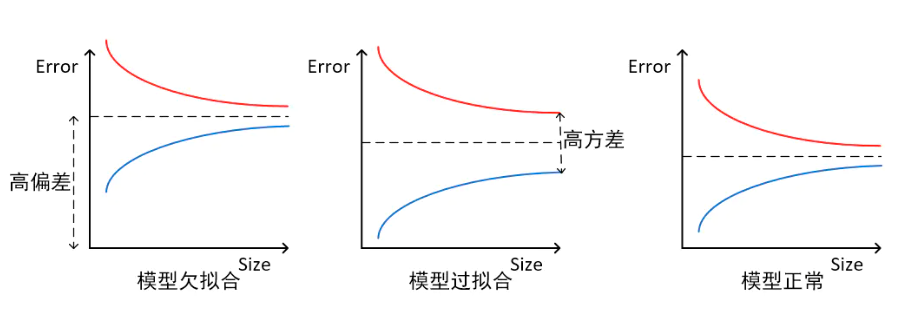
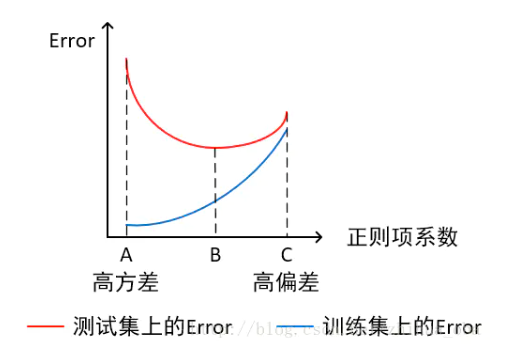
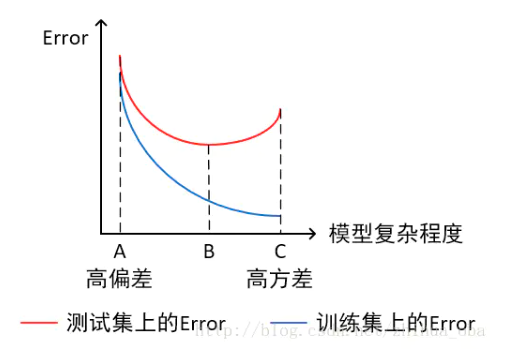
如何解决过拟合与欠拟合
| 方法 | 解决欠拟合 | 解决过拟合 |
|---|---|---|
| 增加模型复杂度 | 增加参数数量、层数、非线性激活函数等,提高模型拟合能力 | - |
| 特征处理 | 通过特征工程增加更多、更有区分性的特征,提高模型表达能力 | 通过特征选择、降维等方法,减少模型的特征维度,降低过拟合风险 |
| 正则化 | 减小正则化强度,以防止模型欠拟合 | 增加正则化项,限制特征权重,降低过拟合风险 |
| 增加数据量 | 增加训练数据,扩大模型覆盖范围,提高泛化能力 | 增加训练数据量,减少过拟合风险 |
| 集成学习 | 采用集成学习(Bagging、Boosting、Stacking等),融合多模型优点 | - |
| 增加噪声 | - | 增加一些噪声使模型更鲁棒,降低过拟合风险 |
| 早停法 | - | 监控验证集性能,当性能下降时停止训练,避免过拟合 |
| Dropout | - | 在神经网络中随机丢弃神经元,降低模型复杂度,降低过拟合风险 |
| 数据增强 | - | 通过旋转、平移、缩放等变换增加训练数据多样性,降低过拟合风险 |
什么叫正则化?
正则化是防止过拟合的技术。常见方法有
L1正则化(Lasso):引入参数绝对值和,实现特征选择,产生稀疏解。
L2正则化(Ridge):引入参数平方和,平滑特征权重分布,提高泛化能力。
Elastic Net:结合L1和L2,实现特征选择与泛化能力的平衡。
通过交叉验证、网格搜索等方法调整正则化强度以防止过拟合或欠拟合。
正则化为什么叫正则化?
·正则化(Regularization)之所以叫正则化,是因为它使模型的参数(权重)遵循某种规则(规范),限制模型参数的取值范围,从而降低模型的复杂度。这有助于模型避免过拟合现象,提高模型在新数据上的泛化能力。
K折交叉验证
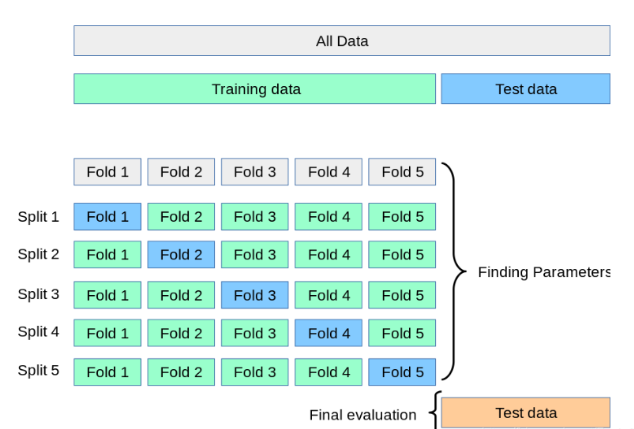
交叉验证是一种评估模型泛化能力的方法。它将数据分成k个子集,每次用k-1个子集训练模型,1个子集验证。重复k次,取平均性能作为评估指标。
这有助于解决过拟合、欠拟合问题和选择最优模型参数。在数据量较小或随机性大时,交叉验证能提高模型稳定性,避免过拟合。
混淆矩阵:
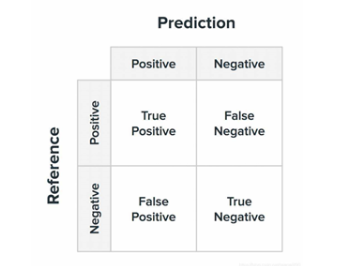
TP 正正例 , FN 错反例
FP 错正例 , TN 正反例
通过混淆矩阵可以计算出多个分类指标

PR曲线
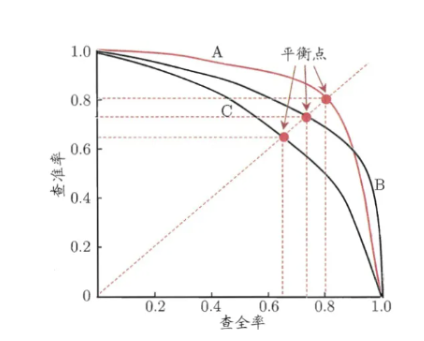
PR曲线是一种用于评估二分类模型性能的工具,横坐标为召回率,纵坐标为精确率,在实际应用中,PR曲线常用于样本不平衡的情况下,评估模型的性能。
PR曲线通常用于二分类问题,因为在二分类问题中,真正例、假正例和假反例的定义比较明确。但是,对于多分类问题,我们也可以将其转化为多个二分类问题,从而使用PR曲线进行评估。例如,在一对多(One-vs-All)策略中,我们可以将一个多分类问题转化为多个二分类问题,然后分别绘制PR曲线,并计算平均准确率(mAP)来评估模型的性能。
PR曲线是根据不同的阈值绘制出来的精度和召回率的曲线,AP是PR曲线下的面积,代表了不同召回率下的平均精度值。mAP是对多个类别的AP进行求平均得到的一个指标,常用于评估目标检测等多类别分类任务的性能。
如何通过P-R曲线比较两个机器学习模型的效果呢?
- 看曲线面积,谁大选谁
- 使用平衡点查准率,值越大越优
ROC曲线
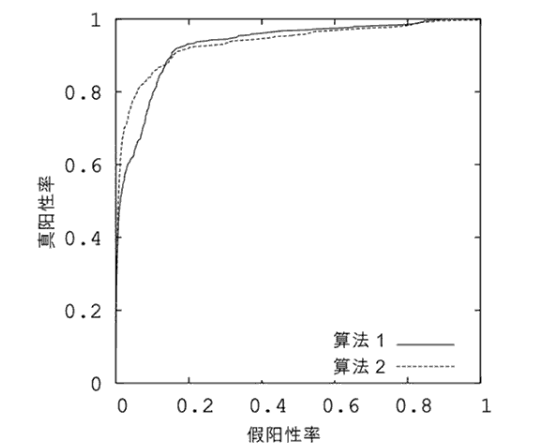
ROC曲线是一种用于评估分类器性能的工具,它通过绘制分类器的真阳率(TPR)与假阳率(FPR)之间的关系曲线来评估分类器的性能。TPR是指正类被正确分类的概率,而FPR则是指负类被错误分类为正类的概率。ROC曲线的斜率越大,说明分类器的性能越好。ROC曲线下面积(AUC)也是一种衡量分类器性能的指标,AUC越大,说明分类器性能越好。
真阳率(TPR)与假阳率(FPR)
真阳率(True Positive Rate,TPR)又称召回率(Recall)指的是在所有实际为正例的样本中,被模型正确预测为正例的样本数占比,即:
TPR = TP / (TP + FN)
其中 TP 表示真正例数,FN 表示假反例数。
假阳率(False Positive Rate,FPR)指的是在所有实际为负例的样本中,被模型错误预测为正例的样本数占比,即:
FPR = FP / (FP + TN)
其中 FP 表示假正例数,TN 表示真反例数。
为什么使用标准差
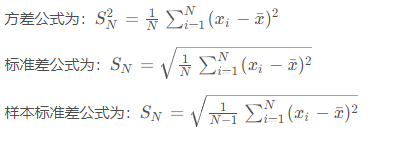
- 数量级一致,更适合对数据样本形成感性认知
- 单位一致
- 符合正太分布
计算样本标准差时,分母上使用的是 n-1,而不是 n。
这是因为样本标准差的计算是基于样本数据的,而样本数据是从总体数据中随机抽取得到的。样本数据中的每个观测值都是独立的,但样本数据的均值和总体数据的均值之间存在一个偏差。这个偏差被称为“自由度”(degrees of freedom),记为 df = n-1。自由度是指在样本数据中可以自由变动的观测值的个数,它的值通常比样本大小小1。
使用 n-1 作为分母可以消除自由度偏差,使得样本标准差能够更准确地估计总体标准差。如果使用 n 作为分母,则样本标准差会偏小,这样可能会导致对总体标准差的估计过于乐观
类别不平衡
类别不平衡(class-imbalance)是指分类任务中不同类别的训练样例数目差别很大的情况。
| 解决方法 | 简要介绍 |
|---|---|
| 数据增强 | 扩大数据集,增加包含小类样本数据的数据,更多的数据能得到更多的分布信息。 |
| 对大类数据欠采样 | 减少大类数据样本个数,使与小样本个数接近。欠采样操作时若随机丢弃大类样本,可能会丢失重要信息。 |
| 对小类数据过采样 | 对小类的数据样本进行采样来增加小类的数据样本个数。 |
| 使用新评价指标 | 在类别不均衡分类任务中,需要使用更有说服力的评价指标来对分类器进行评价。 |
| 选择新算法 | 不同的算法适用于不同的任务与数据,应该使用不同的算法进行比较。 |
| 数据代价加权 | 对分类器的小类样本数据增加权值,降低大类样本的权值,从而使得分类器将重点集中在小类样本身上。 |
| 转化问题思考角度 | 把小类的样本作为异常点,将问题转化为异常点检测或变化趋势检测问题。 |
| 将问题细化分析 | 对问题进行分析与挖掘,将问题划分成多个更小的问题,看这些小问题是否更容易解决。 |
参考文献
目标检测的蓝皮书
