目录

质数

试除法判定质数 

分解质因数

筛质数

约数

试除法求约数

约数个数

约数之和

最大公约数

质数

试除法判定质数 

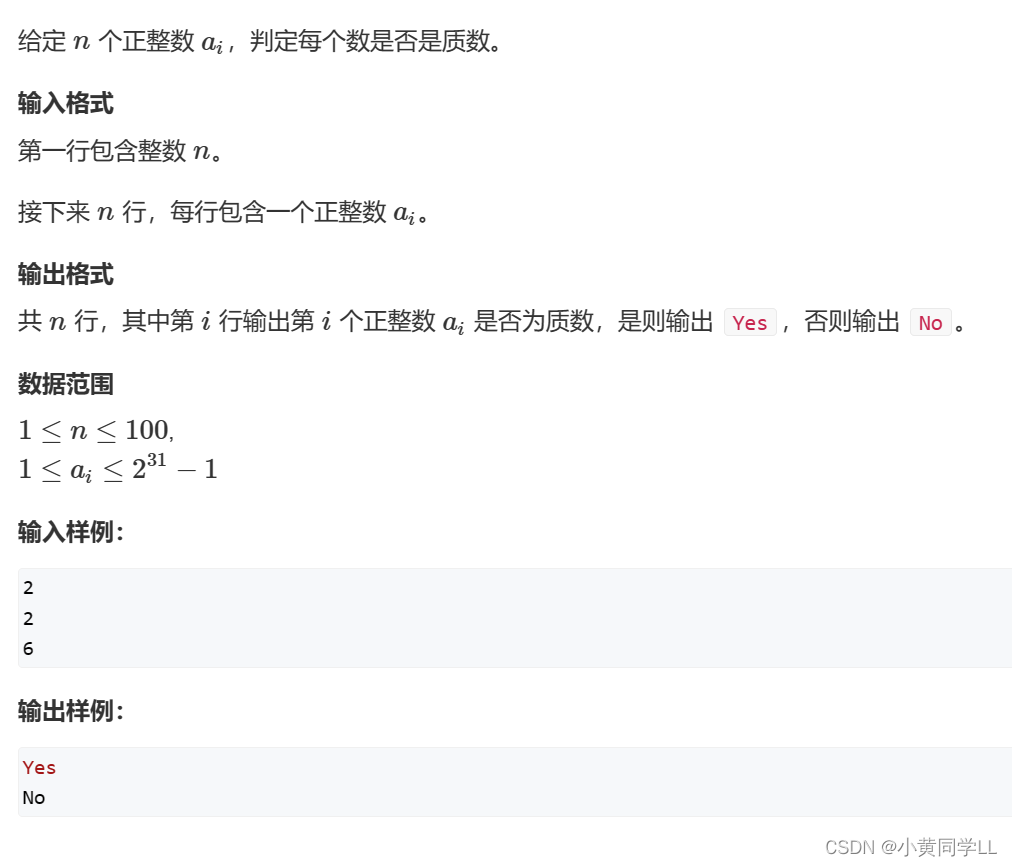
这个算法广为人知，这里就不证明了，解释一下 i<=√n 的写法

1、不推荐写成i<=sqrt(n)

首先需要引入头文件#include麻烦，其次每次循环都要调用sqrt()函数，速度变慢了；

2、强烈不推荐写成 i*i<=n

如果 i 的值比较大， i*i 极有可能有爆int的风险，影响质数判断且很难debug；

3、强烈推荐用 i<=x / i 写法

不需要调用函数且绝对不会有数值过大的风险

#include 
#include using namespace std;bool is_prime(int x)
{if (x < 2) return false;for (int i = 2; i <= x / i; i ++ )//核心操作if (x % i == 0)return false;return true;
}int main()
{int n;cin >> n;while (n -- ){int x;cin >> x;if (is_prime(x)) puts("Yes");else puts("No");}return 0;
}

分解质因数

本词条由“科普中国”科学百科词条编写与应用工作项目 审核 。 

质因子（或质因数）在数论里是指能整除给定正整数的质数。根据算术基本定理，不考虑排列顺序的情况下，每个正整数都能够以唯一的方式表示成它的质因数的乘积。 

即：n=p1^a1 * p2^a2 *p3^a3.....pn^an（p为质数，a为幂）

证明1：

循环里面的 i 一定是一个质数：假如 i 是一个合数，那么它一定可以分解成多个质因子相乘的形式，这多个质因子同时也是 x 的质因子且比 i 要小，而比 i 小的数在之前的循环过程中一定是被条件除完了的，所以 i 不可能是合数，只可能是质数

证明2：

if (x > 1) cout << x << ' ' << 1 << endl;

比sqet(n)大的质因子x最多只有1个，因为如果该质因子x数量大于一个，则x*x>n，是不可能的，所以比sqet(n)大的质因子x最多只有1个

那么我们只需要找小于sqrt（n）的所有质因子，然后如果n的值还大于1，说明仍然存在质因子，又因为大于sqrt（n）的质因子只有一个，所以直接输出该值并标记幂为1

#include 
#include using namespace std;void divide(int x)
{for (int i = 2; i <= x / i; i ++ )if (x % i == 0)//见证明1：如果该条件成立，i一定是质数{int s = 0;while (x % i == 0) x /= i, s ++ ;cout << i << ' ' << s << endl;}if (x > 1) cout << x << ' ' << 1 << endl;//最多只有一个大于平方根下n的质因子（两个相乘就大于n了）cout << endl;
}int main()
{int n;cin >> n;while (n -- ){int x;cin >> x;divide(x);}return 0;
}

筛质数

 诶氏筛法 O(nloglogn)

 根据算术基本定理，不考虑排列顺序的情况下，每个正整数都能够以唯一的方式表示成它的质因数的乘积。 

反向思考：将2到n中，所有质数的倍数删除，那么剩下的就只有质数

#include 
#include using namespace std;const int N= 1000010;int primes[N], cnt;//存质数与质数个数
bool st[N];//用于装合数void get_primes(int n)
{for (int i = 2; i <= n; i ++ ){if (!st[i])//如果不是合数（是质数）{primes[cnt ++ ] = i;//存质数for (int j = i + i; j <= n; j += i)//将质数的倍数（合数）装入st[]st[j] = true;}}//最后primes[]存2到n所有质数，st[]装所有合数
}int main()
{int n;cin >> n;get_primes(n);cout << cnt << endl;return 0;
}

线性筛法 O(n)

if(i%primes[j]==0) break;

分两种情况：

情况1 i%primes[j]!=0

当i%primes[j]!=0时,说明此时遍历到的primes[j]不是i的质因子，那么只可能是此时的primes[j]小于 i 的最小质因子,所以primes[j]*i的最小质因子就是primes[j]; 

情况2 i%primes[j]==0

当有i%primes[j]==0时,说明i的最小质因子是primes[j],因此primes[j]*i的最小质因子也就应该是
prime[j]，当发现primes[j]是i最小质因子的时候,如果再继续进行的话，我们就把 prime[j+1]*i 这个数筛掉了,虽然这个数也是合数，但是我们筛掉它的时候并不是用它的最小质因数筛掉的，而是利用 prime[j+1] 和 i 把它删掉的，也就是说这个数的最小质因数其实是prime[j],如果我们不在这里退出循环的话，我们会发现有些数是被重复删除了的。 

#include 
#include using namespace std;const int N= 1000010;int primes[N], cnt;
bool st[N];void get_primes(int n)
{for (int i = 2; i <= n; i ++ ){if (!st[i]) primes[cnt ++ ] = i;for (int j = 0; primes[j] <= n / i; j ++ )//primes[j]*i<=n 筛掉小于n的合数{st[primes[j] * i] = true;if (i % primes[j] == 0) break;//保证线性筛质数}}
}int main()
{int n;cin >> n;get_primes(n);cout << cnt << endl;return 0;
}

约数

试除法求约数

若 i 是N的约数，则 N/i 也是N的约数。换言之，约数总是成对出现的（(除了对于完全平方数，√N会单独出现)。

#include 
#include 
#include using namespace std;vector get_divisors(int x)
{vector res;for (int i = 1; i <= x / i; i ++ )if (x % i == 0){res.push_back(i);//存储成对出现的约数if (i != x / i) res.push_back(x / i);//除了对于完全平方数，√N会单独出现}sort(res.begin(), res.end());return res;
}int main()
{int n;cin >> n;while (n -- ){int x;cin >> x;auto res = get_divisors(x);for (auto x : res) cout << x << ' ';cout << endl;}return 0;
}

约数个数

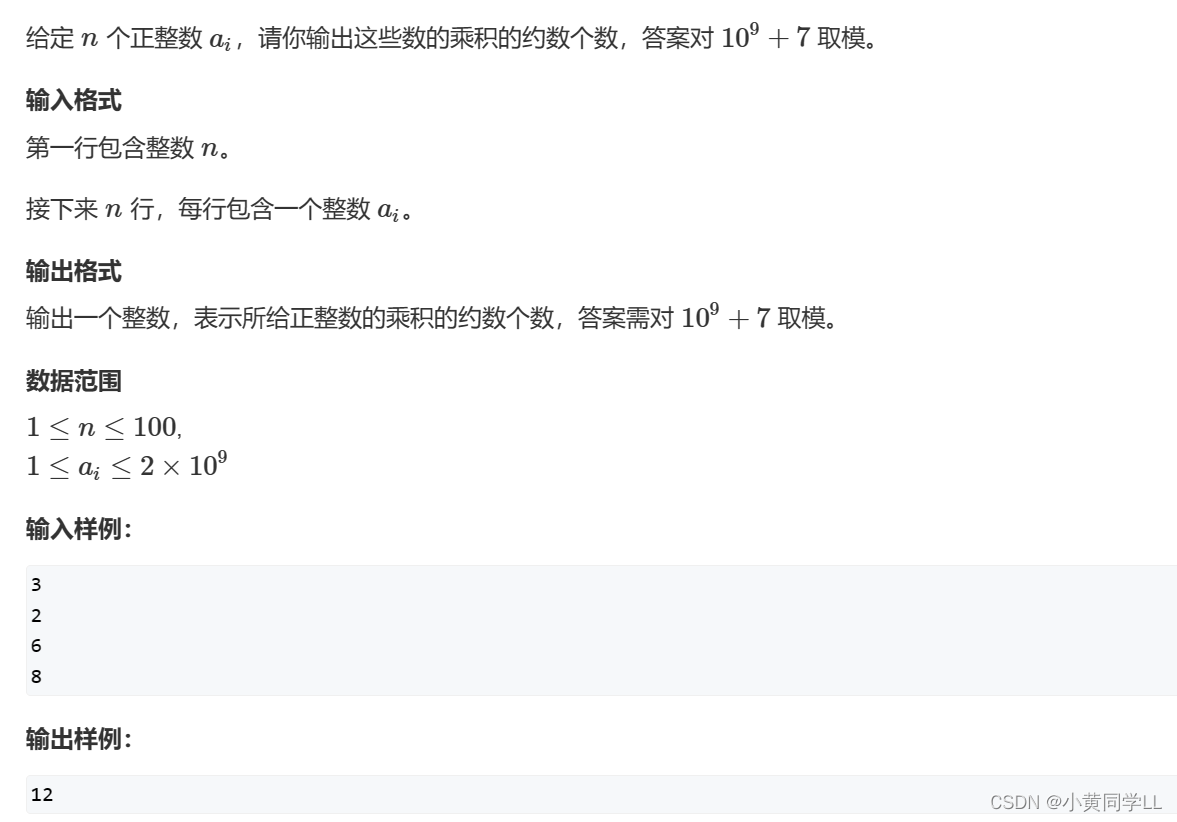
约数个数定理： 

 根据约数个数定理，我们只需要分解质因数，然后直接套公式即可

分解质因数如上质数部分

#include 
#include 
#include 
#include using namespace std;typedef long long LL;const int N = 110, mod = 1e9 + 7;int main()
{int n;cin >> n;unordered_map primes;//存储质数p和对应的幂awhile (n -- ){int x;cin >> x;for (int i = 2; i <= x / i; i ++ )//分解质因数while (x % i == 0){x /= i;primes[i] ++ ;}if (x > 1) primes[x] ++ ;}LL res = 1;for (auto p : primes) res = res * (p.second + 1) % mod;//公式(a1+1)*(a2+1)*....*(ak+1)cout << res << endl;return 0;
}

约数之和

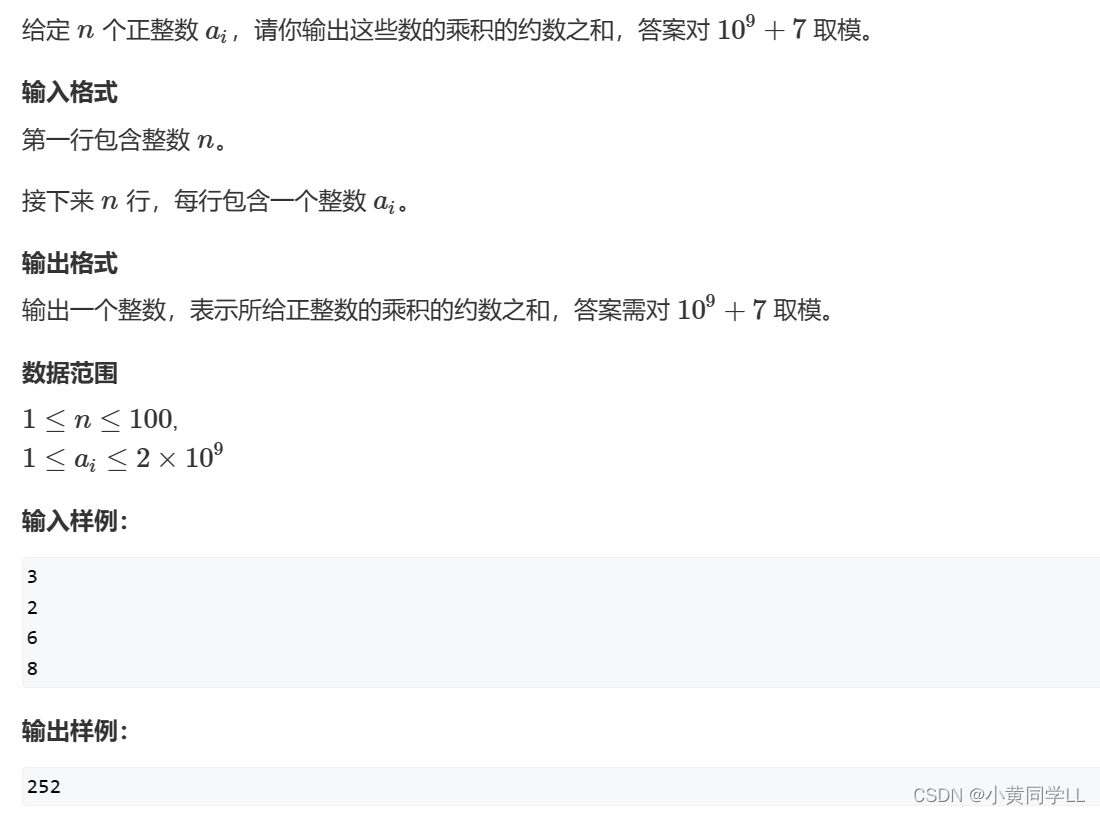
约数和定理_百度百科 (baidu.com)

例题：正整数360的所有正约数的和是多少？

解：将360分解质因数可得

360=2^3*3^2*5^1

由约数和定理可知，360所有正约数的和为

(2^0+2^1+2^2+2^3)×(3^0+3^1+3^2)×(5^0+5^1)=(1+2+4+8)(1+3+9)(1+5)=15×13×6=1170

可知360的约数有1、2、3、4、5、6、8、9、10、12、15、18、

20、24、30、36、40、45、60、72、90、120、180、360；则它们的和为

1+2+3+4+5+6+8+9+10+12+15+18+20+24+30+36+40+45+60+72+90+120+180+360=1170

总结：

分解质因数后，约数和为

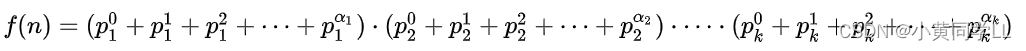
 值得注意的是：

while (b -- ) t = (t * a + 1) % mod;

若b=0，t=1;b=1,t=p+1 以此类推

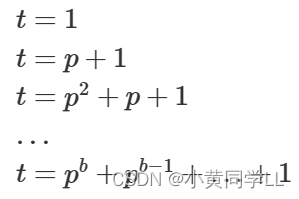
#include 
#include 
#include 
#include using namespace std;typedef long long LL;const int N = 110, mod = 1e9 + 7;int main()
{int n;cin >> n;unordered_map primes;while (n -- ){int x;cin >> x;for (int i = 2; i <= x / i; i ++ )//分解质因数while (x % i == 0){x /= i;primes[i] ++ ;}if (x > 1) primes[x] ++ ;}LL res = 1;for (auto p : primes)//套公式{LL a = p.first, b = p.second;LL t = 1;while (b -- ) t = (t * a + 1) % mod;//求累加res = res * t % mod;//求累乘}cout << res << endl;return 0;
}

最大公约数

辗转相除法求最大公约数，一行代码，背就完事了 

#include 
#include using namespace std;int gcd(int a, int b)
{return b ? gcd(b, a % b) : a;
}int main()
{int n;cin >> n;while (n -- ){int a, b;scanf("%d%d", &a, &b);printf("%d\n", gcd(a, b));}return 0;
}

值得注意的是，可以调用STL；但是速度比自己手写慢个5倍左右！！

#include
#include
using namespace std;！
int n,a,b;
int main() {cin >> n;while(n--){cin >> a >> b;cout << __gcd(a,b) << endl;//调用STL函数}return 0;
}